
프로그래머스 코딩테스트 연습 문제 중에서 2024 KAKAO WINTER INTERNSHIP 문제 세트를 알고리즘 스터디 중에 풀어보게 되었습니다. 해당 문제 세트를 어떻게 접근했고, 어떻게 코드를 작성했는지에 대한 전체 풀이 과정을 포스팅할 예정입니다. 제가 풀이한 과정이 모범 정답 풀이가 아닐 수도 있음을 밝힙니다. 단순히 제가 떠올리고 정답을 받은 풀이임을 알립니다!
1. 가장 많이 받은 선물
다음 달에 선물을 가장 많이 받을 친구가 "다음 달에 받을 선물의 수"를 구해야 한다.
다음 달에 선물을 받기 위해선 다음과 같은 조건이 필요하다.
- 특정 두 사람이 주고 받은 선물 기록이 있다면, 더 많이 준 사람이 다음 달에 선물을 하나 받는다.
- 선물 기록이 같거나 없다면, 선물 지수 (이번 달 준 선물 수 - 이번 달 받은 선물 수) 가 큰 사람이 다음 달에 선물을 하나 받는다.
특정 두 사람이 주고 받은 선물 기록을 조사하는 것은 최대 친구들의 수가 50이므로 여유롭게 가능하다.
나는 3가지 배열을 통해 정답을 구하고자 했다.

(1) 특정 두 사람이 선물을 얼마나 주고 받았는지에 대한 정보 (2차원 배열)
(2) 이번 달 특정 한 사람이 다른 사람에게 준 선물의 수 (1차원 배열)
(3) 이번 달 특정 한 사람이 다른 사람에게 받은 선물의 수 (1차원 배열)
friend_num = len(friends)
table = [[0 for _ in range(friend_num)] for _ in range(friend_num)] # table[i][j] : 친구 i가 친구 j에게 선물을 몇 번 보냈는지
send = [0 for _ in range(friend_num)] # send[i] : 친구 i가 선물을 몇 번 보냈는지
receive = [0 for _ in range(friend_num)] # receive[i] : 친구 i가 선물을 몇 번 받았는지
매개변수로 친구들의 이름이 주어지기 때문에, 친구들의 이름을 인덱스화하여 배열에 접근하기 쉽도록 하고자 했다.
# 친구 이름을 인덱스화 시켜 배열에 저장하기 쉽도록 한다.
def friendIndex(name):
idx = 0
for f in friends:
if f == name:
return idx
idx += 1
for g in gifts:
start, end = g.split()
startIdx = friendIndex(start) # 친구 이름을 번호로 변환
endIdx = friendIndex(end)
table[startIdx][endIdx] += 1
send[startIdx] += 1
receive[endIdx] += 1
당시에 문제 풀이에서 딕셔너리를 잘 안 쓰고자 하는 강박에.. 더 비효율적으로 완전 탐색 함수를 만들어 버렸다 ㅋㅋㅋ 이를 딕셔너리로 작성하면 다음과 같다.
# 친구 이름을 인덱스화 시켜 배열에 저장하기 쉽도록 한다.
friend_index = {}
friend_index_cnt = 0
for g in gifts:
start, end = g.split()
if friend_index.get(start, -1) == -1:
friend_index[start] = friend_index_cnt
friend_index_cnt += 1
if friend_index.get(end, -1) == -1:
friend_index[end] = friend_index_cnt
friend_index_cnt += 1
startIdx = friend_index[start]
endIdx = friend_index[end]
table[startIdx][endIdx] += 1
send[startIdx] += 1
receive[endIdx] += 1
선물을 주고 받은 기록을 다 검토했으니, 이제 다음 달 선물 수를 계산할 차례이다.
next_receive 배열을 사용했다.
next_receive = [0 for _ in range(friend_num)] # next_receive[i] : 친구 i가 다음 달에 선물을 몇 번 받을지
위에서 주어진 조건대로, 모든 친구들의 쌍을 검토해서 다음 달에 선물을 받는 경우를 전부 체크했다.
전부 구했다면, 선물을 가장 많이 받을 친구가 받는 선물의 수를 반환한다.
for start in range(friend_num):
for end in range(start + 1, friend_num): # 모든 친구들의 선물 관계를 1번씩 체크한다. 중복되지 않도록 end 를 start + 1 부터 시작한다.
if table[start][end] == table[end][start]: # 서로 보낸 기록이 없거나 보낸 기록이 같을 경우
start_score = send[start] - receive[start] # 선물 지수 측정
end_score = send[end] - receive[end]
if start_score > end_score: next_receive[start] += 1 # 선물 지수가 더 높은 친구가 다음 달에 한 번 더 받는다.
elif start_score < end_score: next_receive[end] += 1
elif table[start][end] > table[end][start]: next_receive[start] += 1 # 더 많이 보낸 친구가 다음 달에 한 번 더 받는다.
else: next_receive[end] += 1
# 다음 달에 가장 많이 받을 친구의 받을 선물 수
return max(next_receive)
이러면 1번 문제 해결! 단순 구현 + 딕셔너리(이름 해시)로 풀이할 수 있었다.
전체 코드
def solution(friends, gifts):
friend_num = len(friends)
table = [[0 for _ in range(friend_num)] for _ in range(friend_num)] # table[i][j] : 친구 i가 친구 j에게 선물을 몇 번 보냈는지
send = [0 for _ in range(friend_num)] # send[i] : 친구 i가 선물을 몇 번 보냈는지
receive = [0 for _ in range(friend_num)] # receive[i] : 친구 i가 선물을 몇 번 받았는지
# 친구 이름을 인덱스화 시켜 배열에 저장하기 쉽도록 한다.
def friendIndex(name):
idx = 0
for f in friends:
if f == name:
return idx
idx += 1
for g in gifts:
start, end = g.split()
startIdx = friendIndex(start) # 친구 이름을 번호로 변환
endIdx = friendIndex(end)
table[startIdx][endIdx] += 1
send[startIdx] += 1
receive[endIdx] += 1
next_receive = [0 for _ in range(friend_num)] # next_receive[i] : 친구 i가 다음 달에 선물을 몇 번 받을지
for start in range(friend_num):
for end in range(start + 1, friend_num): # 모든 친구들의 선물 관계를 1번씩 체크한다. 중복되지 않도록 end 를 start + 1 부터 시작한다.
if table[start][end] == table[end][start]: # 서로 보낸 기록이 없거나 보낸 기록이 같을 경우
start_score = send[start] - receive[start] # 선물 지수 측정
end_score = send[end] - receive[end]
if start_score > end_score: next_receive[start] += 1 # 선물 지수가 더 높은 친구가 다음 달에 한 번 더 받는다.
elif start_score < end_score: next_receive[end] += 1
elif table[start][end] > table[end][start]: next_receive[start] += 1 # 더 많이 보낸 친구가 다음 달에 한 번 더 받는다.
else: next_receive[end] += 1
# 다음 달에 가장 많이 받을 친구의 받을 선물 수
return max(next_receive)
2. 도넛과 막대 그래프

이 문제를 처음 보고 들었던 궁금증은 2가지 이다. '왜 edge를 100만개나 줄까?' 와 '도넛, 막대, 8자 그래프가 주어진 이유는 무엇일까?' 였다. edge가 100만개이므로 최대한 일차함수 시간 복잡도 안에 끝내자는 마음에, 그래프에 규칙이 있는지 찾아보았다.
핵심은, 정점의 inDegree 와 outDegree 에 있다!
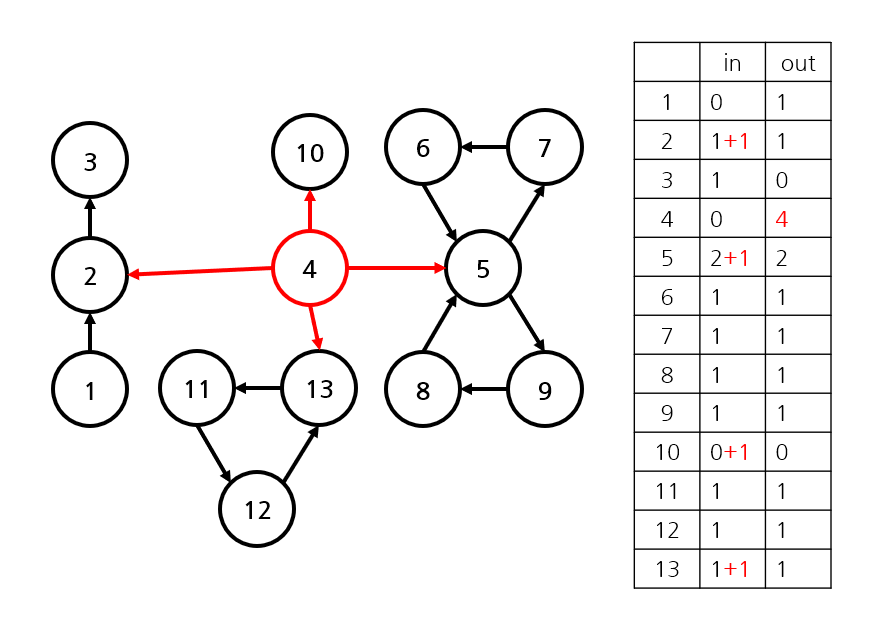
- 그래프의 개수는 최소 2개 이므로, 정점 중에서 inDegree 가 0이고 outDegree 가 2 이상인 정점은 새로 만들어진 정점이다. ( 새로 만들어진 정점 외에, inDegree 가 0이면서 outDegree 가 2 이상인 경우는 없다. )
- 새로 만들어진 정점의 간선들을 제외하며, 다른 정점들의 inDegree 값을 조정한다. 이 때 inDegree 가 0이고 outDegree 가 0인 정점이 된다면 막대 그래프로 판단한다. ( 간선이 없는 정점 )
- 새로 만들어진 정점의 간선을 제외하고, inDegree 가 0이고 outDegree 가 1인 정점의 개수는 막대 그래프의 개수와 같다. (inDegree 가 1이고 outDegree 가 0인 정점의 개수와도 같다. 막대 그래프의 처음 / 끝 정점을 보고 개수를 판단함. )
- 새로 만들어진 정점의 간선을 제외하고, inDegree 가 2이고 outDegree 가 2인 정점의 개수는 8자 그래프의 개수와 같다. ( 8자 그래프의 중간 정점을 보고 8자 그래프 개수를 판단함. )
- 막대 그래프의 개수와 8자 그래프의 개수를 구했다면, 새로 만들어진 정점의 outDegree 에서 (막대 그래프 개수 + 8자 그래프 개수) 를 빼면 도넛 그래프의 개수를 구할 수 있다.
그래프를 유심히 살펴보면 다음과 같은 규칙을 얻을 수 있다!
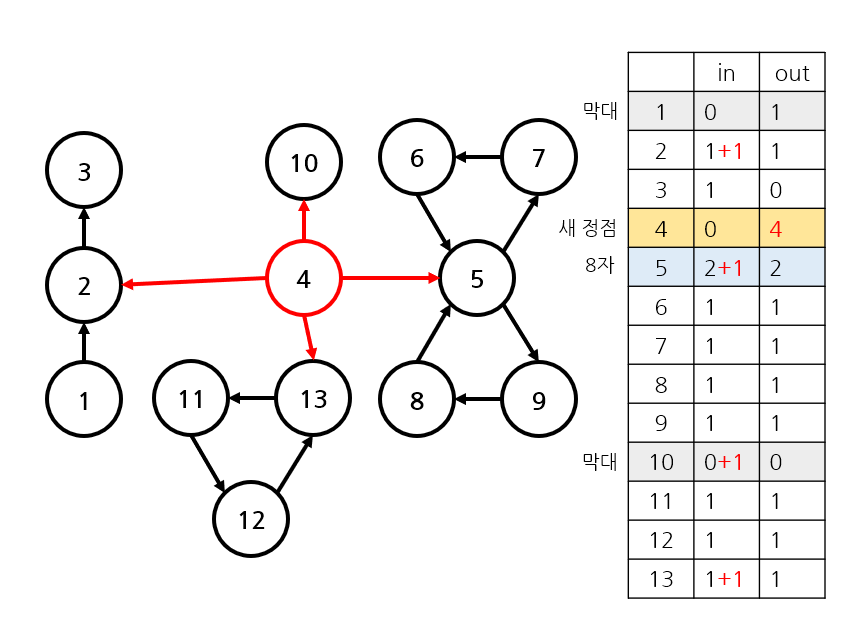
먼저, 정점의 inDegree 와 outDegree 를 센다.
MAX = 1000001
inDegree = [0 for _ in range(MAX)]
outDegree = [0 for _ in range(MAX)]
for e in edges:
# 정점에서 나가는 간선의 개수, 정점으로 들어오는 간선의 개수 카운트
outDegree[e[0]] += 1
inDegree[e[1]] += 1
inDegree 가 0이고 outDegree가 2 이상인 정점은 새로 만들어진 정점이다.
answer = [0, 0, 0, 0]
for i in range(1, MAX):
if inDegree[i] == 0 and outDegree[i] >= 2:
answer[0] = i
break
그래프의 개수를 세기 위해, 새로 만들어진 정점에서 나가는 간선들을 지운다.
새로 만든 정점을 빼는 과정에서, inDegree 와 outDegree 가 모두 0인 정점이 만들어질 수 있다. 이는 막대 그래프로 치기 때문에 막대 그래프 개수를 카운트 한다.
for e in edges:
if e[0] == answer[0]:
inDegree[e[1]] -= 1
# 새로 만든 정점을 빼는 과정에서 홀로 남는 정점을 막대 그래프로 카운트
if inDegree[e[1]] == 0 and outDegree[e[1]] == 0: answer[2] += 1
inDegree 가 0이고 outDegree 가 1이면 막대 그래프, inDegree 가 2이고 outDegree 가 2이면 8자 그래프의 개수이다.
for i in range(1, MAX):
if inDegree[i] == 0 and outDegree[i] == 1: answer[2] += 1
if inDegree[i] == 2 and outDegree[i] == 2: answer[3] += 1
도넛 그래프의 개수는, 새로 만든 정점의 outDegree 에서 막대 그래프의 개수와 8자 그래프의 개수를 뺀 개수이다.
모든 답을 구했다면 답 배열을 반환한다.
answer[1] += outDegree[answer[0]] - (answer[2] + answer[3])
return answer
2번 문제 해결!
전체 코드
def solution(edges):
# 1. inDegree, outDegree 카운트
# 2. 정점 중 inDegree가 0이고 outDegree가 2 이상인 정점이 새로 만든 정점.
# 3. in/out 이 0/1 : 막대 그래프, in/out 이 2/2 : 8자 그래프
# 4. 새로 만든 정점의 outDegree - (막대, 8자 그래프 개수) = 도넛 그래프 개수
answer = [0, 0, 0, 0]
MAX = 1000001
inDegree = [0 for _ in range(MAX)]
outDegree = [0 for _ in range(MAX)]
for e in edges:
outDegree[e[0]] += 1
inDegree[e[1]] += 1
for i in range(1, MAX):
if inDegree[i] == 0 and outDegree[i] >= 2:
answer[0] = i
break
for e in edges:
if e[0] == answer[0]:
inDegree[e[1]] -= 1
# 새로 만든 정점을 빼는 과정에서 홀로 남는 정점을 막대 그래프로 카운트
if inDegree[e[1]] == 0 and outDegree[e[1]] == 0: answer[2] += 1
for i in range(1, MAX):
if inDegree[i] == 0 and outDegree[i] == 1: answer[2] += 1
if inDegree[i] == 2 and outDegree[i] == 2: answer[3] += 1
answer[1] += outDegree[answer[0]] - (answer[2] + answer[3])
return answer
3. 주사위 고르기
백트래킹으로 모든 걸 (주사위 고르기, 주사위 조합에서 나올 수 있는 합 구하기) 해결하려 했지만, 구현한 뒤 시간 복잡도를 계산해보니 연산 횟수가 몇백억이 넘었다.. 최적화를 진행해야 했다.
다음은 내가 떠올린 최적화 아이디어들이다.
1. 10개 주사위 중에서 5개를 고르는 경우의 수는 10C5 (252) 개, 5개 주사위가 만들 수 있는 합은 최대 6^5 (7776) 개이므로, 주사위 조합을 고른 뒤 거기서 나올 수 있는 합들을 저장하는 것은 가능하다!
2. A 주사위 조합에서의 합이 B 주사위 조합을 이길 수 있는 경우의 수를 카운트 해야한다. A의 특정 합보다 작은 B의 합들이 나오는 경우는 이분 탐색으로 구하면 빠르게 구할 수 있을 것 같다.
3. 특정 합이 한 번만 등장하는 것이 아닌, 여러 번 등장할 수 있으므로, 특정 합이 등장한 횟수를 저장해 압축하여 정렬 + 누적 합을 통해 이분 탐색을 진행할 수 있도록 만든다.
4. 주사위의 개수 제한도 많지 않기에, 특정 주사위 조합에 접근하기 쉽도록 비트마스킹을 사용한다.
1. 주사위의 개수는 최대 10개이므로, 1 << 10 로 비트마스킹 하여, 특정 주사위 조합에서 나올 수 있는 합과, 합이 등장한 횟수를 저장한다. 한 번 나온 합을 중복되게 계속 저장하지 않도록 딕셔너리를 활용해, 특정 합이 몇 번 등장했는지를 카운트했다.
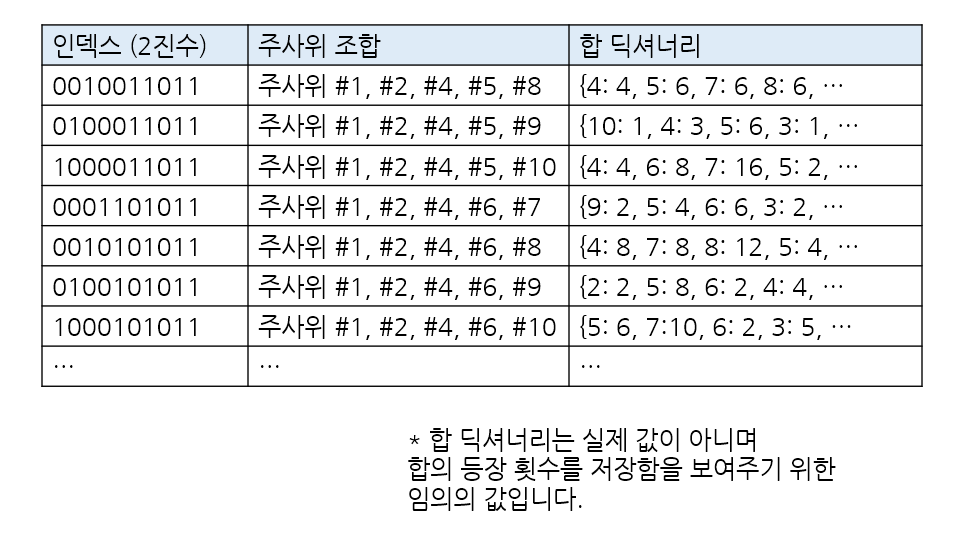
sumsTuple = [{} for _ in range(1 << len(dice))] # 주사위 조합에서 만들 수 있는 합의 개수 튜플, 인덱스는 비트마스킹
2. 백트래킹으로 주사위 조합을 구한 뒤, 해당 주사위 조합에서 나올 수 있는 합을 백트래킹으로 다시 구한다.
중요한 부분은 for element in now: nowIdx |= (1 << element) 이다. 주사위 번호로 2진수 마스크를 만들어 주사위 조합을 구분했다.
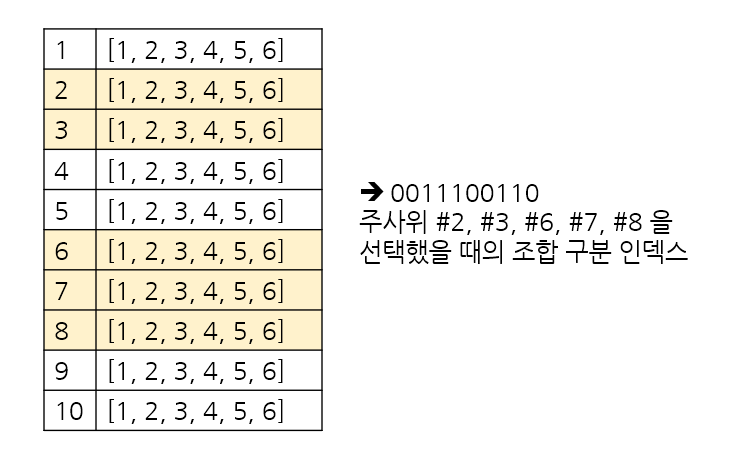
# 주사위 조합에서 나올 수 있는 합 백트래킹
def backtrackingSums(now, arrIdx, diceList, diceIdx):
if arrIdx == len(dice) // 2:
if sumsTuple[diceIdx].get(now, -1) == -1: sumsTuple[diceIdx][now] = 1
else: sumsTuple[diceIdx][now] += 1
return
for i in range(6):
backtrackingSums(now + dice[diceList[arrIdx]][i], arrIdx + 1, diceList, diceIdx)
# 주사위 조합 백트래킹
def backtrackingDice(now, start):
if len(now) == len(dice) // 2:
nowIdx = 0 # 주사위 조합 인덱스
for element in now: nowIdx |= (1 << element)
backtrackingSums(0, 0, now, nowIdx)
return
for i in range(start, len(dice)):
now.append(i)
backtrackingDice(now, i + 1)
now.pop()
backtrackingDice([], 0)
3. 우리는 특정 주사위 조합에서, 나올 수 있는 모든 합 하나하나마다, 상대방 주사위 조합에서 나올 수 있는 합보다 큰 경우의 수를 전부 구해야 한다. 상대방 주사위 조합 인덱스는 2진수 비트 반전 연산으로 빠르게 구할 수 있겠지만, 특정 합이 상대방 주사위 조합을 이길 수 있는 경우를 구하기 위해선, 특정 합이 상대방 주사위 조합에서 나올 수 있는 합보다 큰 경우를 전부 구해야 한다.
주사위 조합에서 나온 합 중 13이 있다고 가정해보자. 이 13이 상대방 조합을 이기기 위해선 상대방 조합에서 나온 합 중 13보다 작은 합이 나온 횟수를 구해야 한다. 12가 5번, 6이 7번... 이걸 전부 세야한다.
이 때, 합을 기준으로 정렬한 뒤, 합이 등장한 횟수를 누적 합으로 만들어 준다면, 이분 탐색으로 특정 합보다 작지만 가장 큰 상대방 합을 구한 뒤, 등장한 횟수 또한 빠르게 구해낼 수 있다.
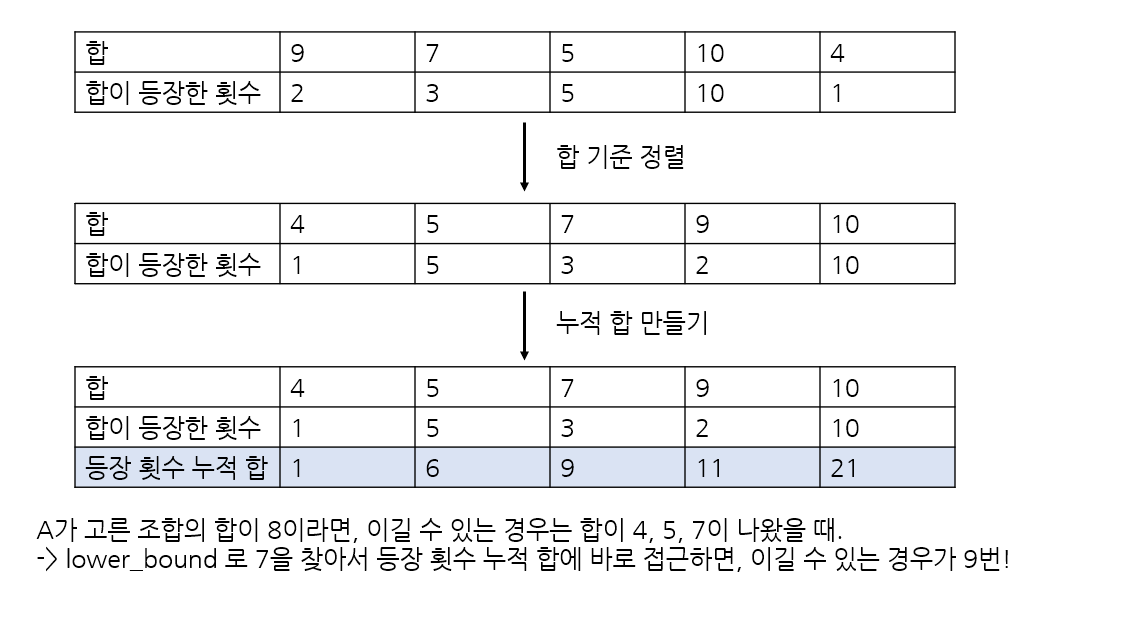
이분 탐색을 위해, 특정 조합 안에서 합을 기준으로 정렬한다.
# 이분 탐색을 위한 key 정렬
for i in range(1 << len(dice)):
sumsTuple[i] = dict(sorted(sumsTuple[i].items()))
4. key와 value를 리스트로 분리한 뒤, 합 등장 횟수 누적 합을 만든다.
# key, value 분리 및 value 누적합 배열 만들기
sumsKey = [list(sumsTuple[i].keys()) for i in range(1 << len(dice))]
sumsValue = [list(sumsTuple[i].values()) for i in range(1 << len(dice))]
sumsPrefixValue = [list(sumsValue[i]) for i in range(1 << len(dice))]
for i in range(1 << len(dice)):
for j in range(1, len(sumsPrefixValue[i])):
sumsPrefixValue[i][j] += sumsPrefixValue[i][j-1]
5. 특정 조합의 모든 합을 순회하면서, 이분 탐색을 통해 특정 합이 이길 수 있는 경우를 전부 합한다.
먼저, 상대 주사위 조합 인덱스는 b = (~a) & ((1 << len(dice)) - 1) 로 구할 수 있다.
bisect 라이브러리의 bisect_left 를 이용해, 특정 합보다 작지만 가장 큰 상대방 합을 구했다.
이길 수 있는 경우는, 내가 고른 특정 합이 등장한 횟수 x 이분 탐색으로 얻은 상대방 합 혹은 그보다 작은 합이 등장한 횟수 를 더해준다. 누적 합과 일반 합을 잘 사용해서 계산한 뒤 더해줘야 한다.
최대로 이길 수 있는 경우의 조합을 발견한다면, 정답 배열을 주사위 조합으로 만들어 반환한다.
answer = []
answerValue = 0
for a in range(1 << len(dice)):
winCnt = 0
for k in range(len(sumsKey[a])):
# b의 주사위 조합은 a의 비트마스킹 반전
b = (~a) & ((1 << len(dice)) - 1)
# 이분 탐색을 이용한 sumsKey[a][k] 보다 작지만 가장 큰 B합 구하기
findALower = bisect_left(sumsKey[b], sumsKey[a][k]) - 1
if findALower < 0: continue
# A 합이 등장한 횟수 * B 합보다 작거나 같은 합들이 등장한 횟수
winCnt += sumsValue[a][k] * sumsPrefixValue[b][findALower]
if winCnt > answerValue:
answerValue = winCnt
# answer 배열 만들기
answer = []
mask = 1
maskCnt = 1
while mask < 1 << len(dice):
if a & mask != 0: answer.append(maskCnt)
mask <<= 1
maskCnt += 1
return answer
이 문제는 백트래킹 + 비트마스킹 + 정렬 + 누적 합 + 이분 탐색으로 풀이 했다. 5개 문제 중에서 가장 많이 고생한 문제.
17% 정답률을 자랑하는 3번 문제 해결!
전체 코드
from bisect import bisect_left
def solution(dice):
# 접근법 1. 백트래킹
# 주사위 고르는 데에 252 * 6**10 까지 가서 순열을 만들어야 함.
# 경우의 수가 100억이 넘어 단순 백트래킹으로 푸는 데에는 한계가 있음.
# 접근법 2. 백트래킹 + 이분 탐색 + 정렬 + 누적 합 + 비트마스킹
# 1. 10개 주사위 중에서 5개 주사위를 고르는 경우의 수는 252개이고,
# 5개 주사위가 만들 수 있는 합의 개수는 6**5 (7776) 개이므로,
# 주사위를 고르고 만들 수 있는 합의 개수를 전부 저장해 놓는 것은 가능하다!
# 2. 백트래킹을 이용해 5개 주사위를 고르고, 그 주사위로 만들 수 있는 합을 전부 구한 뒤 저장한다.
# 3. 합한 값이 중복될 수 있으므로, 딕셔너리를 통해 특정 주사위 조합에서 나오는 합과 그 합이 등장하는 횟수를 저장한다.
# 4. 주사위 조합은, 상대방이 가지게 되는 주사위 조합을 쉽게 구하기 위함과 관리 편의성을 위해 비트마스킹으로 관리한다.
# 5. 5개 주사위 조합을 하나씩 고르고, 나올 수 있는 합을 하나씩 고르면서,
# 상대 주사위 조합의 합에서 A 합보다 적게 나오는 경우의 수를 누적합으로 구해야 한다.
# 6. 딕셔너리의 value 를 따로 분리해 누적합으로 만들어 놓고, key 도 분리하여 이분탐색 용으로 사용한다.
# (특정 A 합보다 작고 최대한 큰 합 이분 탐색으로 구하면, 특정 A 합보다 작은 합이 나올 경우의 수를 누적합으로 구한다.)
# 7. 승리 횟수가 가장 높은 주사위 조합을 구한다.
sumsTuple = [{} for _ in range(1 << len(dice))] # 주사위 조합에서 만들 수 있는 합의 개수 튜플, 인덱스는 비트마스킹
# 주사위 조합에서 나올 수 있는 합 백트래킹
def backtrackingSums(now, arrIdx, diceList, diceIdx):
if arrIdx == len(dice) // 2:
if sumsTuple[diceIdx].get(now, -1) == -1: sumsTuple[diceIdx][now] = 1
else: sumsTuple[diceIdx][now] += 1
return
for i in range(6):
backtrackingSums(now + dice[diceList[arrIdx]][i], arrIdx + 1, diceList, diceIdx)
# 주사위 조합 백트래킹
def backtrackingDice(now, start):
if len(now) == len(dice) // 2:
nowIdx = 0 # 주사위 조합 인덱스
for element in now: nowIdx |= (1 << element)
backtrackingSums(0, 0, now, nowIdx)
return
for i in range(start, len(dice)):
now.append(i)
backtrackingDice(now, i + 1)
now.pop()
backtrackingDice([], 0)
# 이분 탐색을 위한 key 정렬
for i in range(1 << len(dice)):
sumsTuple[i] = dict(sorted(sumsTuple[i].items()))
# key, value 분리 및 value 누적합 배열 만들기
sumsKey = [list(sumsTuple[i].keys()) for i in range(1 << len(dice))]
sumsValue = [list(sumsTuple[i].values()) for i in range(1 << len(dice))]
sumsPrefixValue = [list(sumsValue[i]) for i in range(1 << len(dice))]
for i in range(1 << len(dice)):
for j in range(1, len(sumsPrefixValue[i])):
sumsPrefixValue[i][j] += sumsPrefixValue[i][j-1]
answer = []
answerValue = 0
for a in range(1 << len(dice)):
winCnt = 0
for k in range(len(sumsKey[a])):
# b의 주사위 조합은 a의 비트마스킹 반전
b = (~a) & ((1 << len(dice)) - 1)
# 이분 탐색을 이용한 sumsKey[a][k] 보다 작지만 가장 큰 B합 구하기
findALower = bisect_left(sumsKey[b], sumsKey[a][k]) - 1
if findALower < 0: continue
# A 합이 등장한 횟수 * B 합보다 작거나 같은 합들이 등장한 횟수
winCnt += sumsValue[a][k] * sumsPrefixValue[b][findALower]
if winCnt > answerValue:
answerValue = winCnt
# answer 배열 만들기
answer = []
mask = 1
maskCnt = 1
while mask < 1 << len(dice):
if a & mask != 0: answer.append(maskCnt)
mask <<= 1
maskCnt += 1
return answer
4. n + 1 카드게임
문제를 읽고 처음엔 그리디로 접근했는데, 무조건 n + 1를 만족하는 카드 쌍을 발견할 때마다 사는 것보다 더 효율적으로 할 수 있는 방법이 있었다. 즉 고려해야 할 경우가 더 있었다.
접근을 바꿔서, 탑다운 DP로 코인을 ? 개 소모했을 때 최대 몇 라운드까지 버틸 수 있는지 DP에 상태를 표시하는 방법을 선택했다.
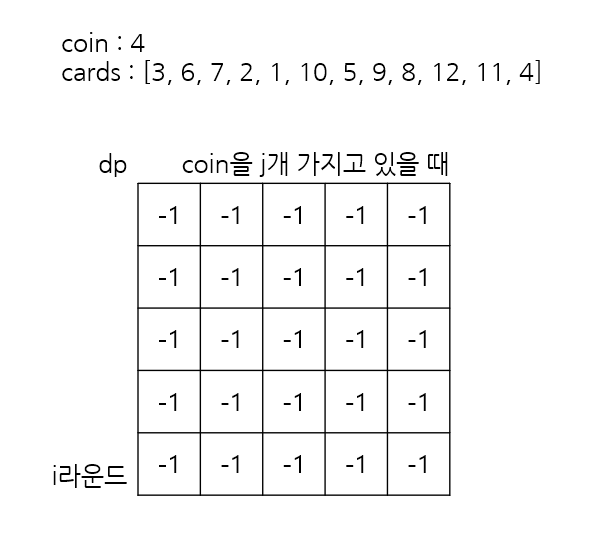
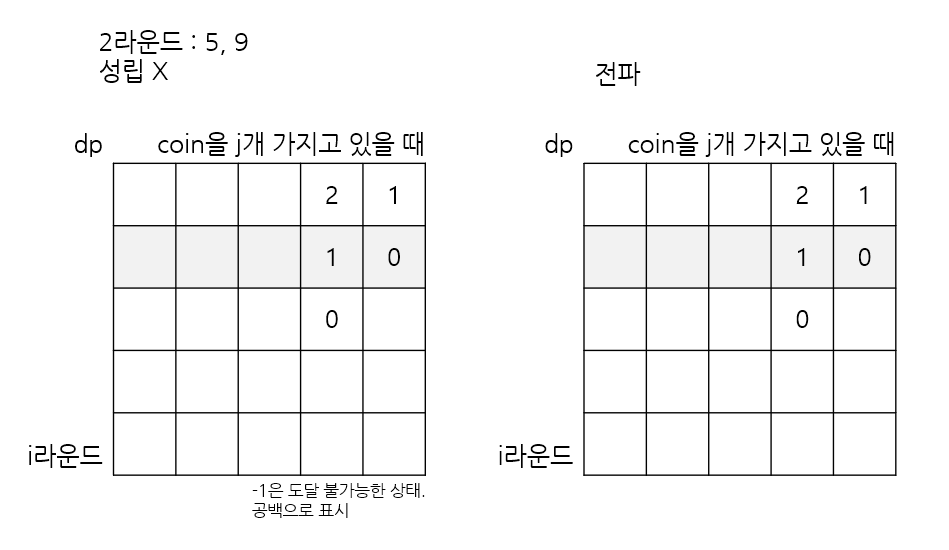
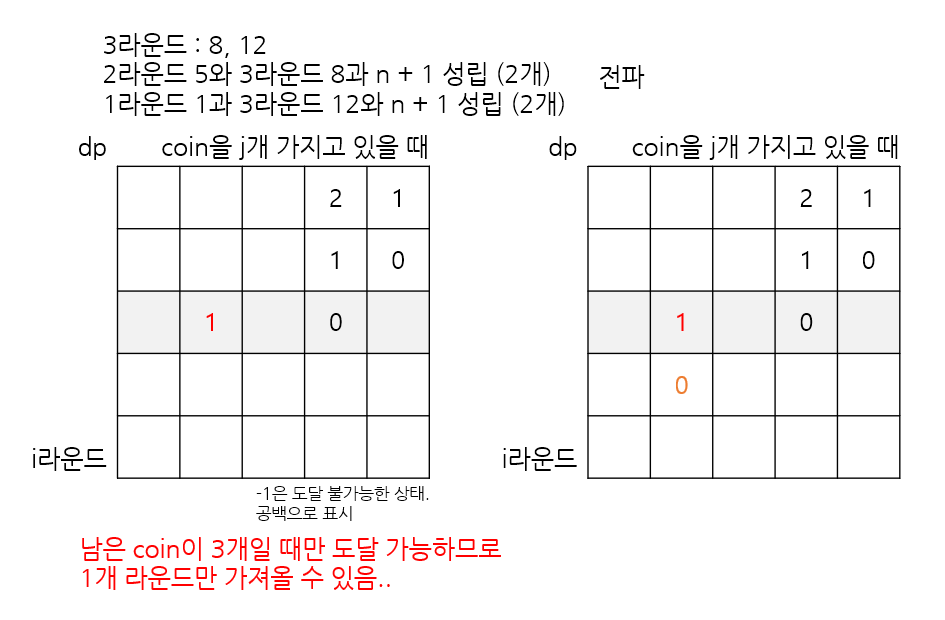
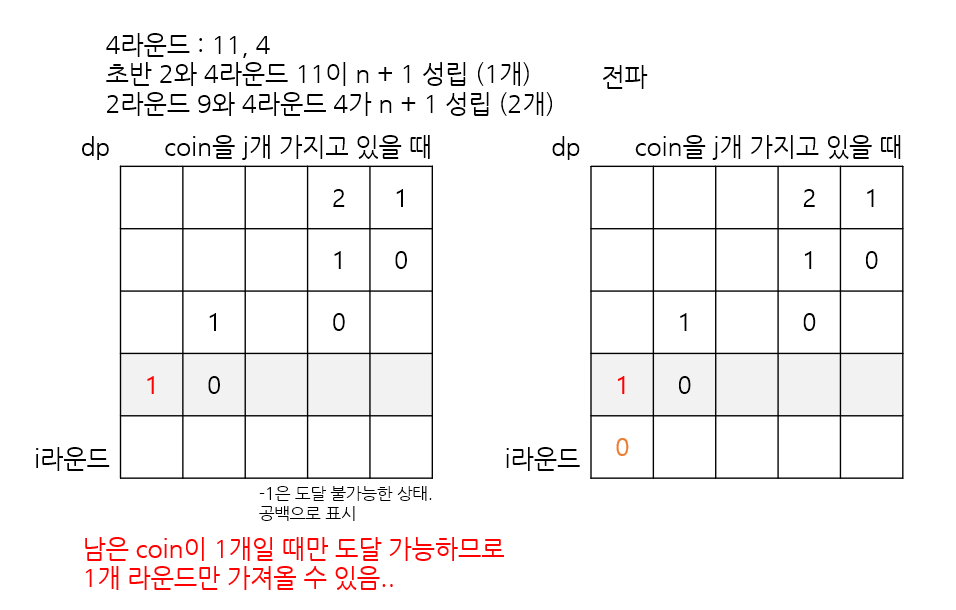
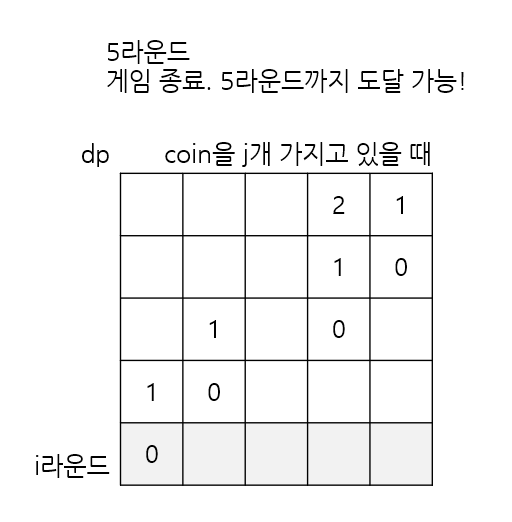
다음과 같은 아이디어를 활용해 구현해보자.
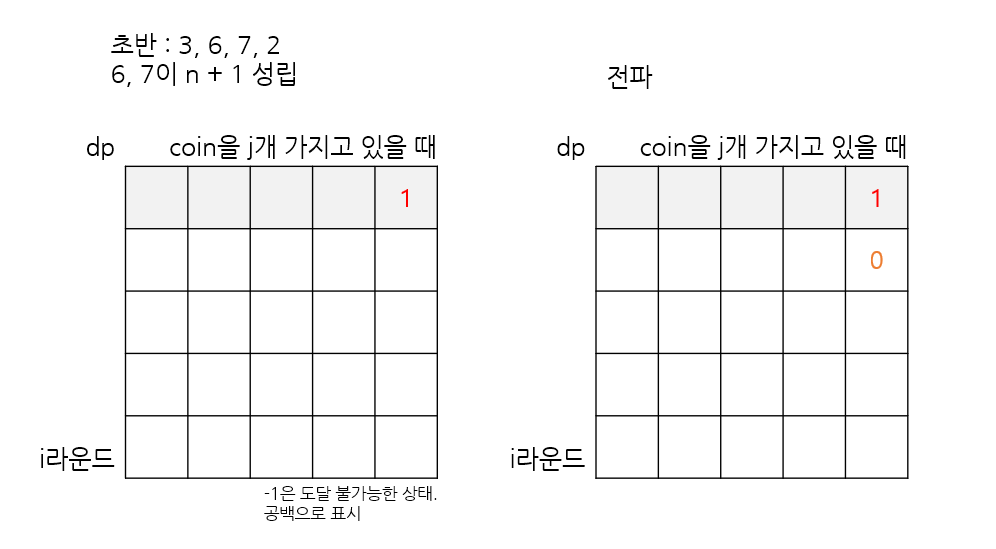
맨 처음에 가질 수 있는 카드 쌍 중에서, n + 1 을 만족하는 카드 쌍이 있다면, 그 카드 쌍으로 1라운드 씩 버틸 수 있기에 체크한 뒤 dp[0][coin] (1라운드에 코인 coin 개를 가지고 있는 상태) 에 표시한다.
n = len(cards)
rounds = n // 3
# dp[i][j] : i라운드에 코인 j 개를 가지고 있을 때, 앞으로 최대 dp[i][j] 개 라운드를 버틸 수 있음.
# -1 : 도달 불가능한 상태
dp = [[-1 for _ in range(coin+1)] for _ in range(rounds + 1)]
dp[0][coin] = 0 # 1라운드에 코인 coin 개를 가지고 있을 때는 도달 가능한 상태.
for i in range(n // 3 - 1):
for j in range(i + 1, n // 3):
# 초반에 가지는 n // 3 개의 카드 중에서 n + 1을 만족하는 카드 쌍이 있는지 확인
if cards[i] + cards[j] == n + 1:
dp[0][coin] += 1 # 그 카드 쌍으로 1라운드 씩 버틸 수 있음!
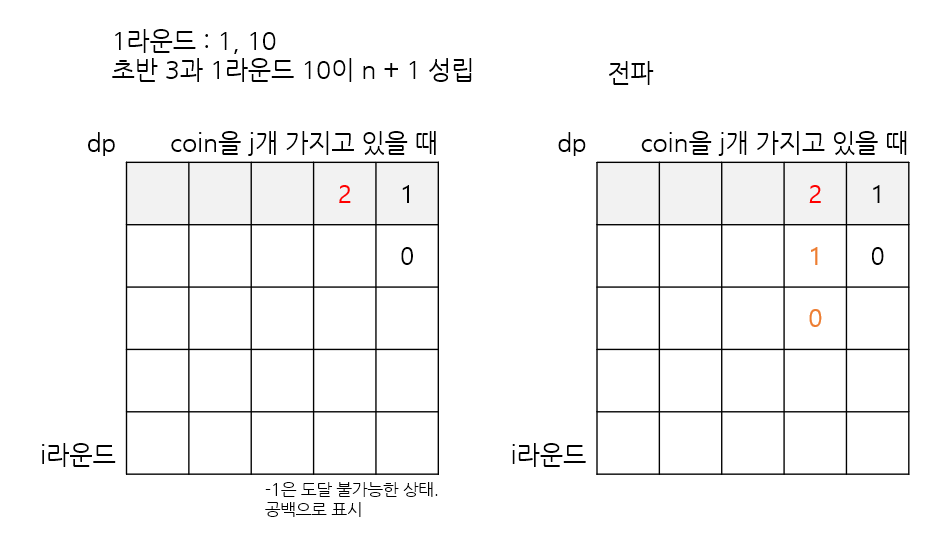
앞으로 이 상태에서 코인을 소모하지 않을 때의 도달 가능한 상태를 쭉 전파한다.
# 1라운드에 코인을 소모하지 않고 dp[0][coin] 라운드를 버틸 수 있다면,
# 2라운드에 코인을 소모하지 않았을 땐 dp[0][coin] - 1 라운드를 더 버틸 수 있고,
# 3라운드에 코인을 소모하지 않았을 땐 dp[0][coin] - 2 라운드를 더 버틸 수 있고...
# 앞으로 코인을 소모하지 않을 때의 도달 가능한 상태를 전파한다.
for k in range(dp[0][coin]): dp[k+1][coin] = dp[0][coin] - 1 - k
이제, 라운드를 하나씩 거쳐가며 받는 카드를 활용해 더 효율적인 라운드 전개 상황을 찾아내야 한다.
1. 이전 라운드에 받았었는데 지금 받은 카드와 합하면 n + 1 이 만족하는 경우, 코인 2개를 소모하여 1라운드를 더 버틸 수 있음을 표시한다.
2. 1라운드 이전에 맨 처음에 이미 보유 중인 카드가 지금 받은 카드와 합하면 n + 1 이 만족하는 경우, 코인 1개를 소모하여 1라운드를 더 버틸 수 있음을 표시한다.
# c : i라운드에 받는 카드
# p : i라운드 이전에, c와 합했을 때 n + 1을 만족하는 카드
for c in range(rounds + (i * 2), rounds + (i * 2) + 2):
for p in range(rounds + (i * 2)):
if cards[c] + cards[p] == n + 1:
if p < rounds: # p가 1라운드 이전에 받은 카드라면 이미 보유 중. 코인 1개 소모 (c 구매)
for j in range(1, coin + 1):
if dp[i][j] >= 0: # i라운드에 코인 j개를 소유할 수 있다면
dp[i][j-1] = max(dp[i][j-1], dp[i][j] + 1) # 코인 1개 소모하고 1라운드 추가
else: # p는 1라운드부터 받은 카드. 이전에 구매 했어야 하므로 코인 2개 소모 (c와 p 구매)
for j in range(2, coin + 1):
if dp[i][j] >= 0:
dp[i][j-2] = max(dp[i][j-2], dp[i][j] + 1)
혹은, 특정 라운드에 받은 카드 두 개가 n + 1을 만족하는 경우도 고려한다.
if cards[rounds + (i * 2)] + cards[rounds + (i * 2) + 1] == n + 1: # 받은 두 개가 n + 1을 만족한다면
for j in range(2, coin + 1):
if dp[i][j] >= 0:
dp[i][j-2] = max(dp[i][j-2], dp[i][j] + 1)
코인이 ? 개 남은 상태마다 버틸 수 있는 라운드가 있다면, 다음 라운드로 도달 가능함을 전파한다.
# 현재 라운드에서, 각 코인마다 버틸 수 있는 라운드가 있다면 다음 라운드로 전파하여 도달 가능함을 알리기
for j in range(coin + 1):
for k in range(dp[i][j]):
if i + 1 + k > rounds: break
dp[i+1+k][j] = dp[i][j] - 1 - k
현재 상태에서 1라운드도 버틸 수 없다면 게임을 종료해야 한다.
# 카드를 전부 구매했지만, 1라운드도 버틸 수 없다면 종료
survived = 0
for j in range(coin + 1):
if dp[i][j] > 0:
survived = 1
break
if survived == 0:
break
4번 문제 해결!
전체 코드
def solution(coin, cards):
answer = 0
# 접근법 1.
# 그리디 : 당장 n + 1을 만족하는 카드 쌍을 무작정 많이 사두는 것보다 더 효율적인 방법이 존재함.
# 예를 들면, (초반에 받은 카드 1장 + k라운드에 뽑은 카드 1장 == n + 1) 2쌍 으로 2라운드 버티기 가능
# 접근법 2.
# 탑다운 DP : 코인을 ? 개 소모했을 때 최대 몇 라운드까지 버틸 수 있는지를 DP에 상태 표시
# 그리디 접근법보다 더 다양한 경우를 고려 가능함. 공간 복잡도 또한 만족함.
n = len(cards)
rounds = n // 3
# dp[i][j] : i라운드에 코인 j 개를 가지고 있을 때, 앞으로 최대 dp[i][j] 개 라운드를 버틸 수 있음.
# -1 : 도달 불가능한 상태
dp = [[-1 for _ in range(coin+1)] for _ in range(rounds + 1)]
dp[0][coin] = 0 # 1라운드에 코인 coin 개를 가지고 있을 때는 도달 가능한 상태.
for i in range(n // 3 - 1):
for j in range(i + 1, n // 3):
# 초반에 가지는 n // 3 개의 카드 중에서 n + 1을 만족하는 카드 쌍이 있는지 확인
if cards[i] + cards[j] == n + 1:
dp[0][coin] += 1 # 그 카드 쌍으로 1라운드 씩 버틸 수 있음!
# 1라운드에 코인을 소모하지 않고 dp[0][coin] 라운드를 버틸 수 있다면,
# 2라운드에 코인을 소모하지 않았을 땐 dp[0][coin] - 1 라운드를 더 버틸 수 있고,
# 3라운드에 코인을 소모하지 않았을 땐 dp[0][coin] - 2 라운드를 더 버틸 수 있고...
# 앞으로 코인을 소모하지 않을 때의 도달 가능한 상태를 전파한다.
for k in range(dp[0][coin]): dp[k+1][coin] = dp[0][coin] - 1 - k
for i in range(rounds + 1):
# 다음 라운드 도달
answer += 1
# 마지막 라운드에 도착했다면 종료한다.
if i == rounds: break
# c : i라운드에 받는 카드
# p : i라운드 이전에, c와 합했을 때 n + 1을 만족하는 카드
for c in range(rounds + (i * 2), rounds + (i * 2) + 2):
for p in range(rounds + (i * 2)):
if cards[c] + cards[p] == n + 1:
if p < rounds: # p가 1라운드 이전에 받은 카드라면 이미 보유 중. 코인 1개 소모 (c 구매)
for j in range(1, coin + 1):
if dp[i][j] >= 0: # i라운드에 코인 j개를 소유할 수 있다면
dp[i][j-1] = max(dp[i][j-1], dp[i][j] + 1) # 코인 1개 소모하고 1라운드 추가
else: # p는 1라운드부터 받은 카드. 이전에 구매 했어야 하므로 코인 2개 소모 (c와 p 구매)
for j in range(2, coin + 1):
if dp[i][j] >= 0:
dp[i][j-2] = max(dp[i][j-2], dp[i][j] + 1)
# NOTE
# for j in range(1, coin + 1) 을 역순으로 진행하면 값이 계속 전파되는 논리 오류 발생.
# 1부터 시작해야 제일 코인이 없을 때부터 시작해서 정확한 전파가 가능함.
if cards[rounds + (i * 2)] + cards[rounds + (i * 2) + 1] == n + 1: # 받은 두 개가 n + 1을 만족한다면
for j in range(2, coin + 1):
if dp[i][j] >= 0:
dp[i][j-2] = max(dp[i][j-2], dp[i][j] + 1)
# 현재 라운드에서, 각 코인마다 버틸 수 있는 라운드가 있다면 다음 라운드로 전파하여 도달 가능함을 알리기
for j in range(coin + 1):
for k in range(dp[i][j]):
if i + 1 + k > rounds: break
dp[i+1+k][j] = dp[i][j] - 1 - k
# 카드를 전부 구매했지만, 1라운드도 버틸 수 없다면 종료
survived = 0
for j in range(coin + 1):
if dp[i][j] > 0:
survived = 1
break
if survived == 0:
break
return answer
5. 산 모양 타일링
3번, 4번보다 쉬운 문제였다. 타일링 유형은 워낙 DP 문제 풀어본 게 있어서 그런지, 바로 아이디어가 떠올랐다.
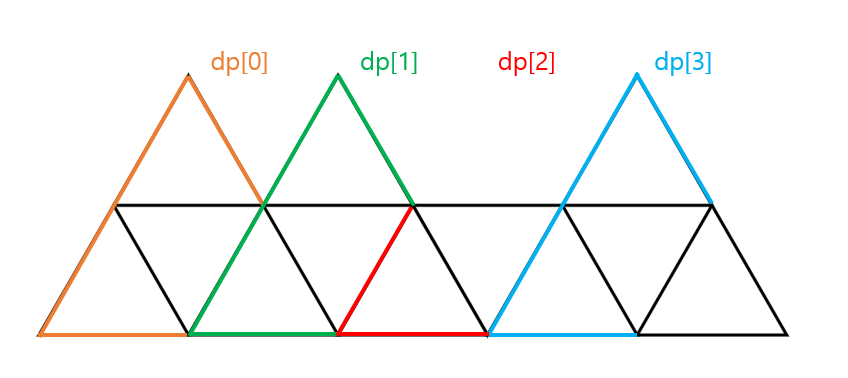
먼저, 산 모양 하나씩을 dp 테이블의 한 행으로 간주했다.
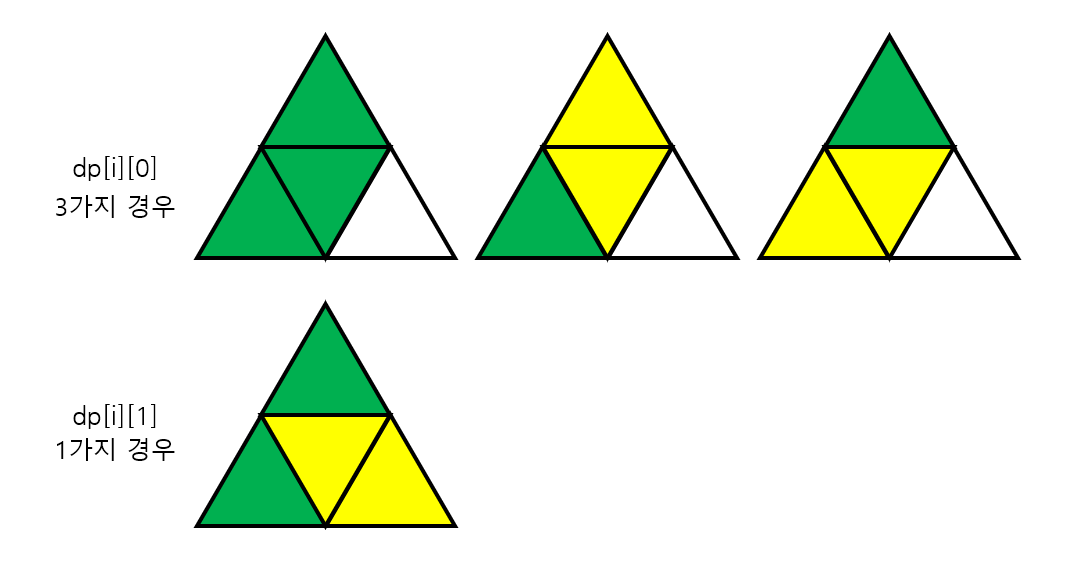
그리고, 다음 행을 침범하는 마름모 타일을 놓는 경우와, 그 외의 경우 (다음 행을 침범하지 않는 경우) 로 2열을 만들었다.
점화식은 다음과 같이 구성했다. 먼저 현재 행에 산 모양이 있는 경우이다.
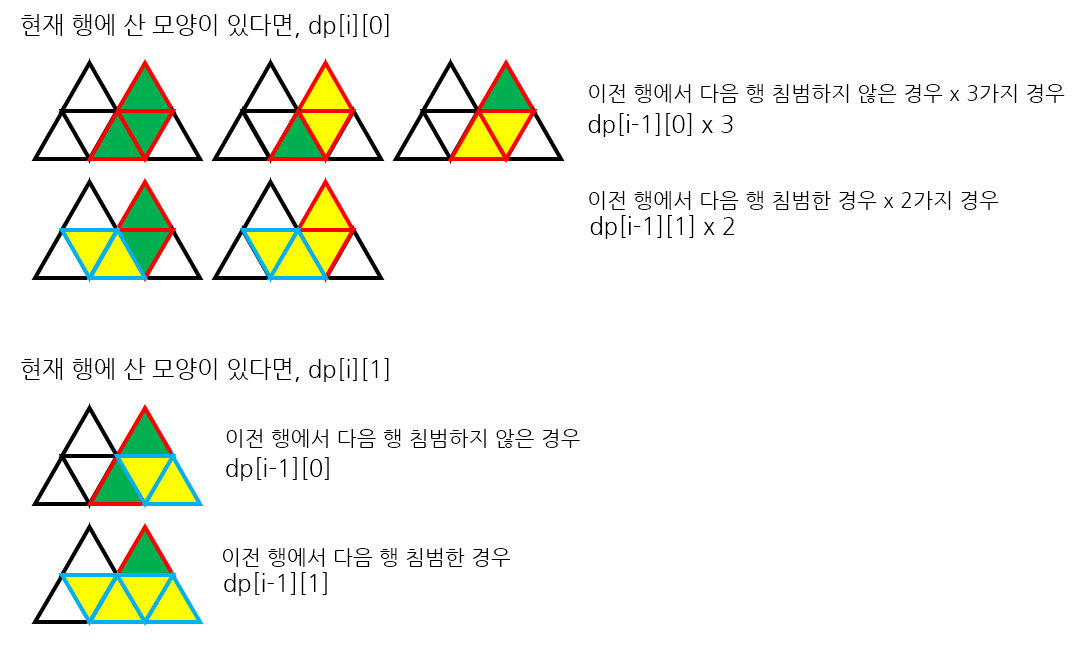
다음은 현재 행에 산 모양이 없는 경우이다.
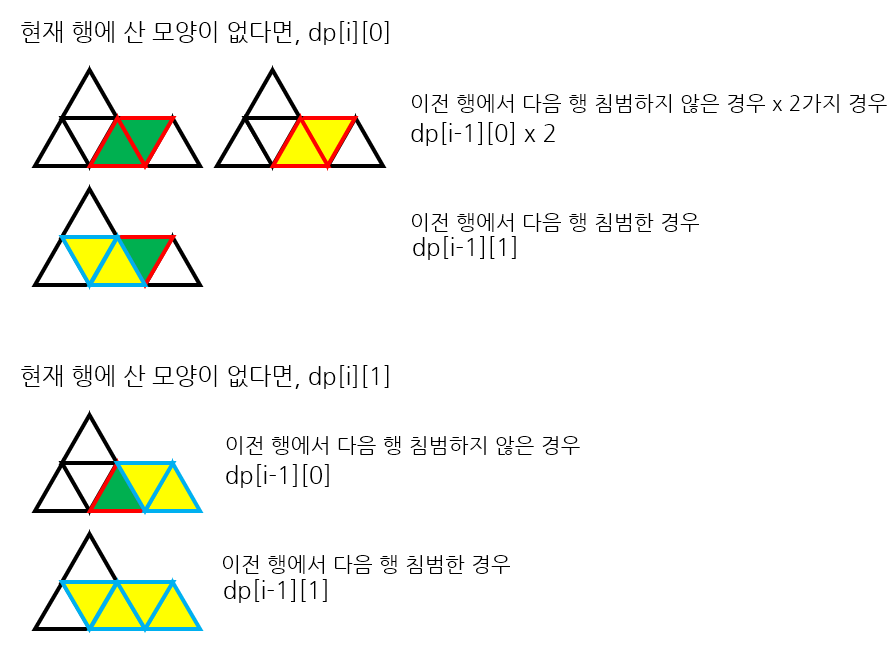
이를 그대로 구현하면 5번 문제도 해결!
전체 코드
def solution(n, tops):
answer = 0
dp = [[0, 0] for _ in range(n)]
if tops[0] == 0: dp[0] = [2, 1]
else: dp[0] = [3, 1]
for i in range(1, n):
if tops[i] == 0:
dp[i] = [((dp[i-1][0] * 2) + (dp[i-1][1])) % 10007, (dp[i-1][0] + dp[i-1][1]) % 10007]
else:
dp[i] = [((dp[i-1][0] * 3) + (dp[i-1][1] * 2)) % 10007, (dp[i-1][0] + dp[i-1][1]) % 10007]
answer = sum(dp[n-1]) % 10007
return answer
전체적으로 문제가 재밌었다. 알고리즘을 잘 응용하면 수월하게 풀이할 수 있는 난이도의 문제로 편성된 것 같다.
실제 테스트에서 해당 문제 세트 시간은 5시간이 주어진다고 하는데, 시간 안에 내가 다 풀 수 있을지는 잘 모르겠다. (부대 안에서 며칠동안 조금씩 조금씩 풀었던지라 시간 가늠이 잘 되지 않았다.)
이번 기회에 처음으로 기업 코테 문제를 풀어보았는데, 앞으로도 다른 코테 기출문제 세트로 더 연습해보고 싶다!