
문제
그래프 G는 정점의 집합 V와 간선의 집합 E로 이루어져 있고, G = (V, E)로 나타낸다. 대부분의 경우에 V와 E는 명시되어 있다. 일부 그래프의 경우에는 집합이 명시되어 있지 않다. 예를 들어, 순열 그래프는 간선의 집합이 명시되어 있지 않다.
{1, 2, 3, 4, 5}로 이루어진 두 순열 (2, 5, 4, 1, 3)과 (1, 5, 3, 2, 4)가 있다. 평행선을 그리고, 그 위에 순열에 적힌 숫자 순서대로 정점을 그린다. 그 다음 같은 숫자끼리 선분을 연결한다. 아래 그림과 같이 교차하는 선분의 쌍은 총 여섯 개라는 것을 알 수 있다.
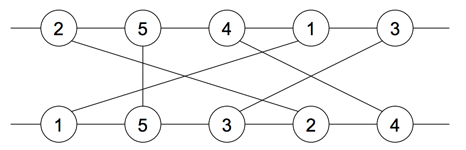
교차하는 쌍은 순열 그래프의 간선이 된다. 순열 그래프의 정점은 숫자가 되고, 간선은 교차하는 쌍이 된다. 위의 예를 이용해 순열 그래프를 만들면 V = {1, 2, 3, 4, 5}, E = {(1,2), (1,4), (1,5), (2,3), (2,5), (3,4)}. 위의 두 순열을 이용해 순열 그래프를 그리면 아래 그림과 같이 된다.

{1, 2, ..., n}으로 이루어진 두 순열이 주어졌을 때, 두 순열을 이용해 만든 순열 그래프의 간선의 개수를 구하는 프로그램을 작성하시오. 예를 들어, (2, 5, 4, 1, 3)과 (1, 5, 3, 2, 4)로 만든 순열 그래프의 간선의 개수는 6개이다.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스의 첫째 줄에는 n이 주어진다. 둘째 줄과 셋째 줄에는 두 순열이 주어진다. 순열은 {1, 2, ..., n}으로 이루어져 있고, 공백으로 구분되어져 있다. (1 ≤ n ≤ 100,000)
출력
각 테스트 케이스 마다, 입력으로 주어진 두 순열로 만든 순열 그래프의 간선의 개수를 출력한다.
풀이 과정
교차 선분 세그먼트 트리 문제이다. 테스트 케이스마다 윗 줄의 노드가 아랫 줄의 어디랑 연결되어 있는지를 잘 체크한다면 크게 어렵지 않다.
#include <stdio.h>
#define QUERY_SIZE 100001
int query[QUERY_SIZE] = { 0, };
int dest[QUERY_SIZE] = { 0, };
int tree[QUERY_SIZE * 4] = { 0, };
void init(int start, int end, int idx) {
if (start == end) {
tree[idx] = 0;
return;
}
int mid = (start + end) / 2;
init(start, mid, idx * 2);
init(mid + 1, end, idx * 2 + 1);
tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
}
void update(int start, int end, int idx, int what) {
if (what < start || end < what) return;
if (start == end) {
tree[idx] += 1;
return;
}
int mid = (start + end) / 2;
update(start, mid, idx * 2, what);
update(mid + 1, end, idx * 2 + 1, what);
tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
}
long long interval_sum(int start, int end, int idx, int left, int right) {
if (end < left || right < start) return 0;
if (left <= start && end <= right) return tree[idx];
int mid = (start + end) / 2;
return interval_sum(start, mid, idx * 2, left, right) + interval_sum(mid + 1, end, idx * 2 + 1, left, right);
}
int main(void) {
int test;
scanf("%d", &test);
while (test--) {
int n;
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &query[i]);
dest[i] = 0;
}
int num;
for (int i = 0; i < n; i++) {
scanf("%d", &num);
dest[num] = i;
}
init(0, n - 1, 1);
long long result = 0;
for (int i = 0; i < n; i++) {
update(0, n - 1, 1, dest[query[i]]);
if (dest[query[i]] != n - 1)
result += interval_sum(0, n - 1, 1, dest[query[i]] + 1, n - 1);
}
printf("%lld\n", result);
}
return 0;
}'(예전 글) > BOJ' 카테고리의 다른 글
| [ BOJ ] 16978 : 수열과 쿼리 22 ( PLATINUM 4 ) / C (0) | 2023.04.10 |
|---|---|
| [ BOJ ] 1517 : 버블 소트 ( PLATINUM 5 ) / C (0) | 2023.04.09 |
| [ BOJ ] 17407 : 괄호 문자열과 쿼리 ( PLATINUM 3 ) / C (0) | 2023.04.08 |
| [ BOJ ] 4779 : 칸토어 집합 ( SILVER 3 ) / Python (0) | 2023.04.08 |
| [ BOJ ] 1572 : 중앙값 ( PLATINUM 5 ) / C (0) | 2023.04.07 |