강한 연결 요소 (SCC, Strongly Connected Component) 란, 유향 그래프에서 정점의 부분집합이 부분집합 내의 다른 모든 정점에 대해 방문 가능한 경우를 말한다.

쉽게 말해 사이클이 생기는 그룹을 엮으면 강한 연결 요소가 된다. 다음 그래프에서 사이클이 생기는 그룹을 엮어보자.

이 사이클이 생기는 그룹을 하나의 정점으로 보고 문제를 해결해야 하는 경우가 생길 수 있다. 따라서 이렇게 엮은 그룹들을 정점으로 치환하면 다음과 같은 그래프로 볼 수 있다.

정점 안에서 엮여진 하위 정점들은 그 정점 안이라면 언제든 방문 가능하다. 이렇게 강한 연결 요소로 묶으면 사이클이 없는 유향 그래프로 바라볼 수 있다는 특징이 있다.
이제 SCC 를 두 가지 방법으로 구현해보자.
타잔 알고리즘
SCC 를 구현하는 방법 중 DFS 를 한 번 사용하는 알고리즘으로, 코드가 순차적이라 구현하기에는 코사라주보다 살짝 양이 많다.
DFS를 통해 정점을 탐색하면서, 사이클을 발견하면, 방문해왔던 정점들을 저장한 스택에서 사이클 시작점까지 정점을 빼서 강한 연결 요소로 묶으면 된다! 사이클을 발견하기 위해 우리는 정점에 고유 번호를 부여하고, 탐색 중에 "이전에 방문했지만 아직 연결 요소로 묶지 않은 정점"을 발견한다면 사이클로 인식하고 같은 고유 번호로 변환시켜, 유니온 파인드처럼 사이클 안 정점들을 그룹화 시킬 것이다.
타잔 알고리즘의 DFS 과정은 다음과 같다.

첫 번째로 방문한 정점에 고유 번호를 부여하고, 스택에 넣는다.

주변에 아직 방문하지 않은 정점이 있다면, DFS를 진행한다. 처음 방문했다면 고유 번호를 부여하고 스택에 넣는다.
5번 정점, 4번 정점, 3번 정점까지 계속 진행해보자.

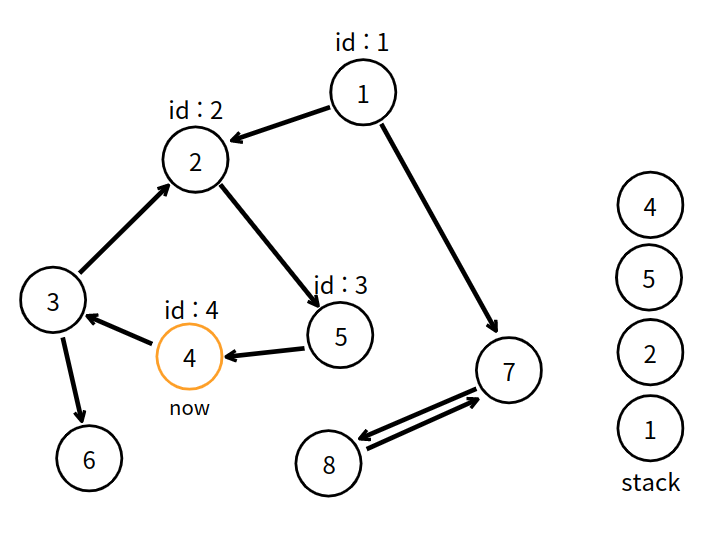
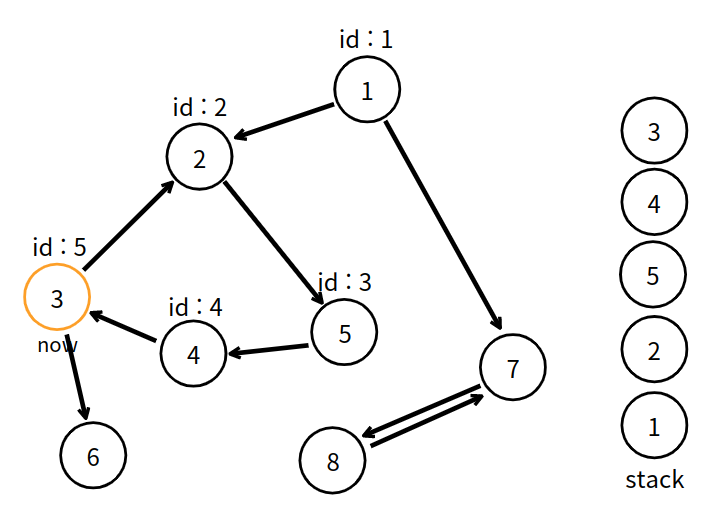
3번 정점에서 이웃 정점을 둘러보던 도중, 방문은 했지만 아직 스택에 남아있는 2번 정점을 발견했다. 이때 현재 방문하고 있는 정점의 고유 번호보다 이웃 정점에 부여된 고유 번호가 더 작다면, 더 작은 고유 번호로 변환해서 같은 집함임을 기록해야 한다. 즉, 5번 정점의 고유 번호를 2로 바꾼다.
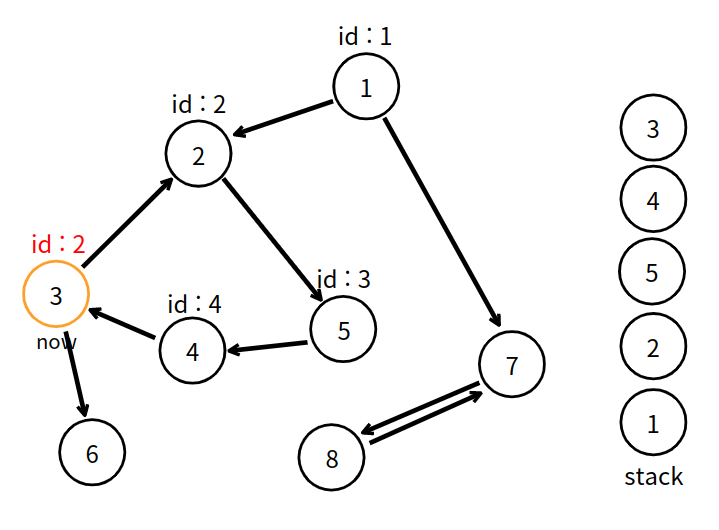
다른 이웃 정점인 6번 정점이 남았으니 마저 탐색해보자.
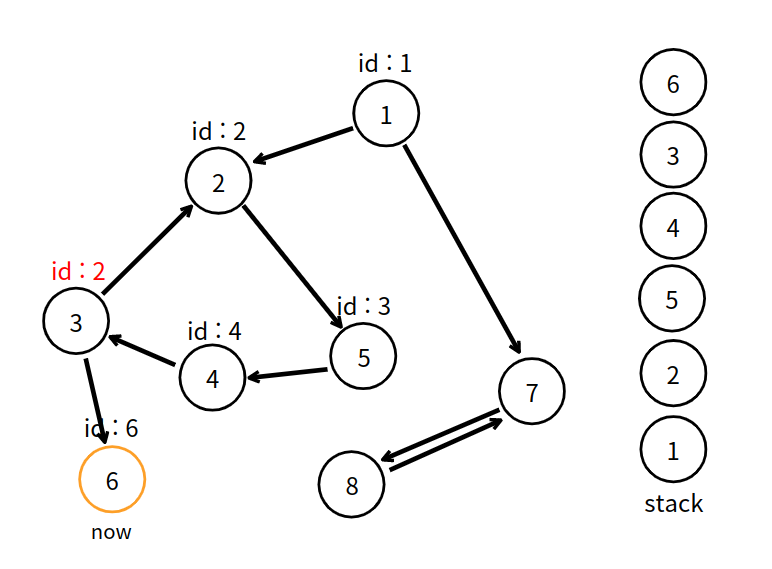
6번 정점은 더이상 이웃 정점이 없으므로 탐색을 마쳤다.
여기서부터 중요하다. 해당 정점에서 이웃 정점이 없어 탐색을 마친다면, 정점 자신이 "강한 연결 요소로 연결을 시작하는 부모 정점"인지, 즉 사이클을 시작하는 정점인지를 판단해야 한다.
예를 들면, 3번 정점은 고유 번호 2를 가졌지만, 이 사이클은 2번 정점에서 연결을 시작한다. (아직 사이클 시작점이 아님) 즉 3번 정점은 강한 연결 요소로 연결을 시작하는 부모 정점이 아니다. 여기서, 6번 정점은 동일한 고유 번호 6을 가졌으므로 강한 연결 요소로 연결을 시작하는 부모 정점이다!
특정 정점에서 탐색이 끝났을 때 자신의 고유 번호가 변하지 않는다면, 방문했을 때 부여받은 고유 번호를 유지하고 있다면, "사이클이 시작되는" 고유 번호가 가장 작은 부모 정점이다! 사이클을 발견한 것으로 판단하고 강한 연결 요소로 엮기를 시작한다!
강한 연결 요소로 연결하기 위해선, 현재 쌓여있는 스택에서 자신과 동일한 정점이 나올 때 까지 스택에서 빼면, 스택에서 뺀 정점들은 한 강한 연결 요소 집합이 된다. (사이클에 있는 정점 전부 털기) 현재 스택의 맨 위는 6번 정점이고, 동일한 정점이므로 일단 1개의 정점을 가진 강한 연결 요소를 찾아낸 것이다.
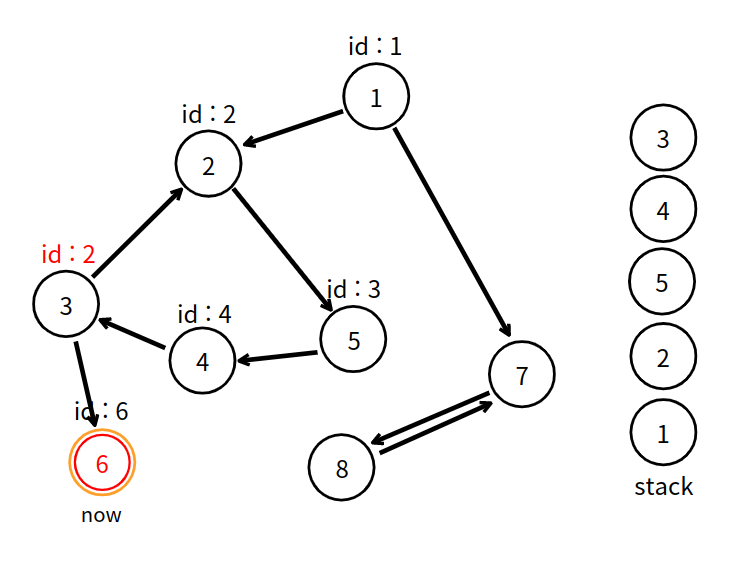
6번 정점은 스택의 맨 위에 있었으므로 1개의 정점을 스택에서 뺐다. 따라서 1개의 정점을 가진 강한 연결 요소로 처리했다. 탐색이 끝났다면 이전 정점에게 더 작은 고유 번호의 가능성을 알려주기 위해 고유 번호를 전달한다.
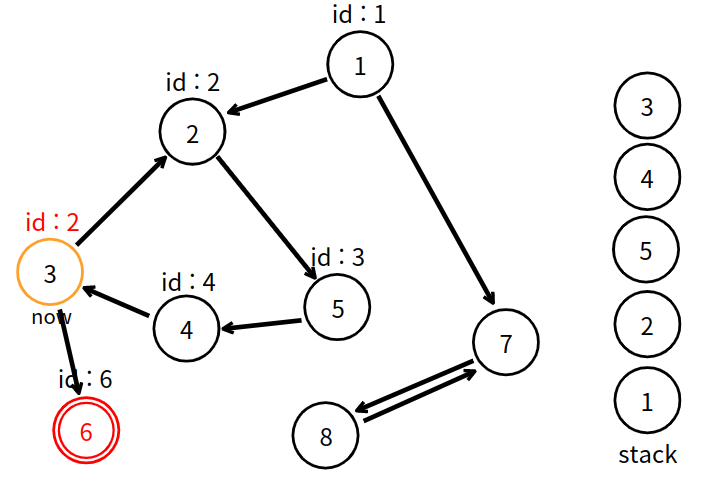
3번 정점은 이미 2라는 적은 고유 번호를 가지고 있으므로, 6번 정점에게 받은 6 대신 2를 유지한다.
탐색이 끝났고, 자신이 부여받았던 번호인 3과 고유 번호인 2는 같지 않으므로 강한 연결 요소로 연결을 시작하는 정점이 아니다. 아까 말했듯이, 고유 번호가 2인 정점이 "강한 연결 요소"로 연결을 시작할 것이다. 이전 4번 정점한테 고유 번호를 전달한다.
탐색이 끝났다고 스택에서 정점을 제거하지 않는다. 스택은 "방문을 했지만 강한 연결 요소를 찾지 못한 정점들" 을 저장하기 때문에, 이후에 사이클을 발견한다면 강한 연결 요소로 차례대로 연결할 수 있도록 일단 둔다.
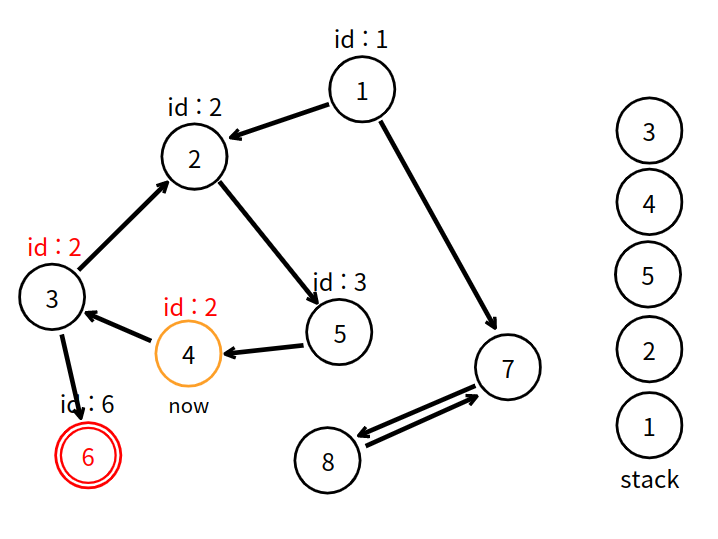
4번 정점이 더 적은 고유 번호인 2번을 발견했다. id 는 2가 된다.
탐색이 끝났고, 자신이 부여받았던 번호인 4와 고유 번호인 2는 같지 않으므로 강한 연결 요소로 연결을 시작하는 정점이 아니다. 이전 정점한테 고유 번호를 전달한다.
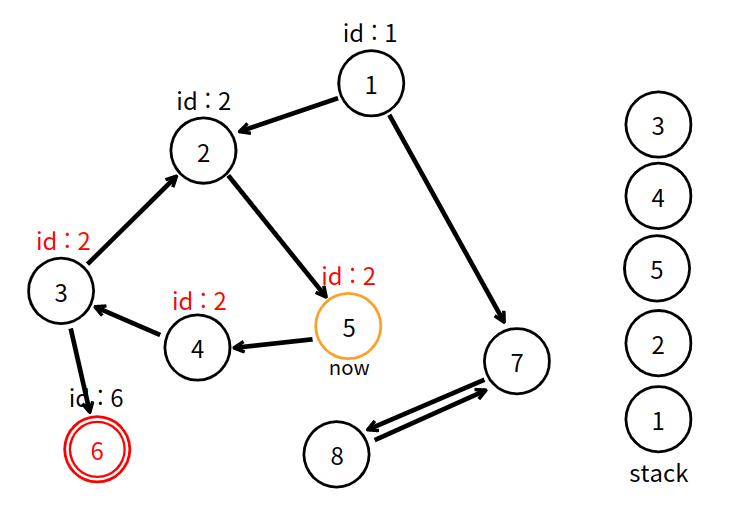
5번 정점이 더 적은 고유 번호인 2번을 발견했다. id 는 2가 된다.
탐색이 끝났고, 자신이 부여받았던 번호인 5와 고유 번호인 2는 같지 않으므로 강한 연결 요소로 연결을 시작하는 정점이 아니다. 이전 정점한테 고유 번호를 전달한다.
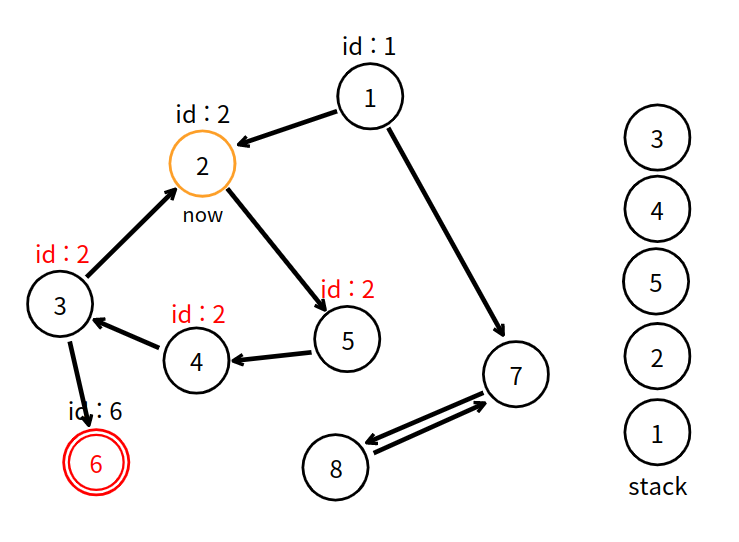
2번 정점은 고유 번호가 2이므로 5번 정점에게 받은 2로 바뀌지 않는다.
탐색이 끝났고, 자신이 부여받았던 번호인 2과 고유 번호인 2는 같으므로 강한 연결 요소로 연결을 시작한다. 사이클 시작점이다!
현재 쌓여있는 스택에서 자신과 동일한 정점이 나올 때 까지 스택에서 뺀다.
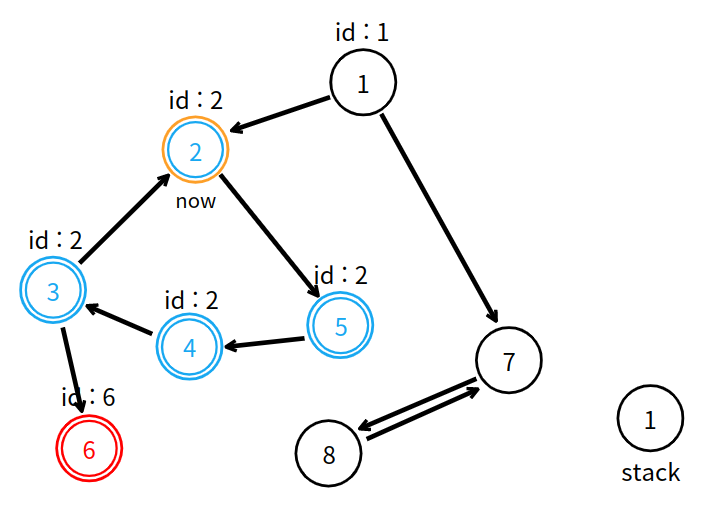
4개의 정점을 가진 강한 연결 요소를 발견했다. 이전 정점한테 고유 번호를 전달한다.
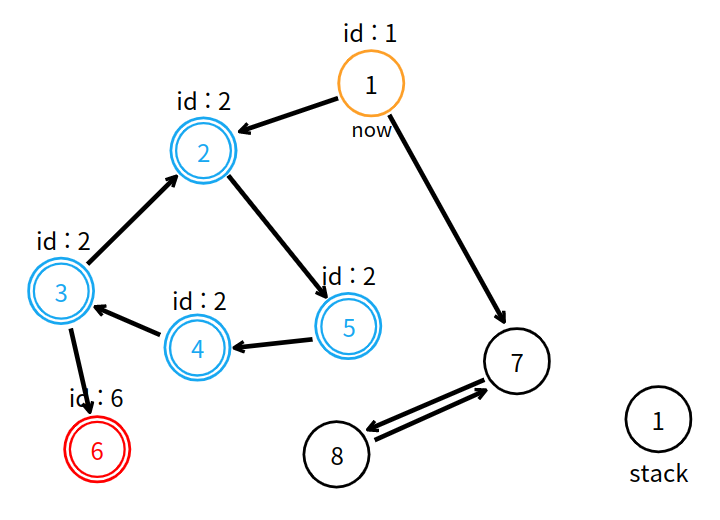
1번 정점은 2번 정점에게 고유 번호 2를 받았지만, 부여된 고유 번호 1이 이미 작으므로, 다음 탐색을 진행한다. 방문하지 않은 7번 정점을 탐색한다.
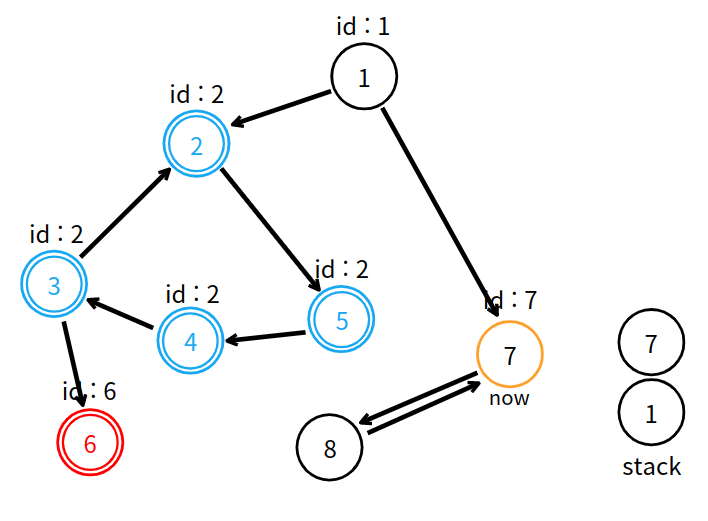
방문하지 않은 8번 정점을 탐색한다.
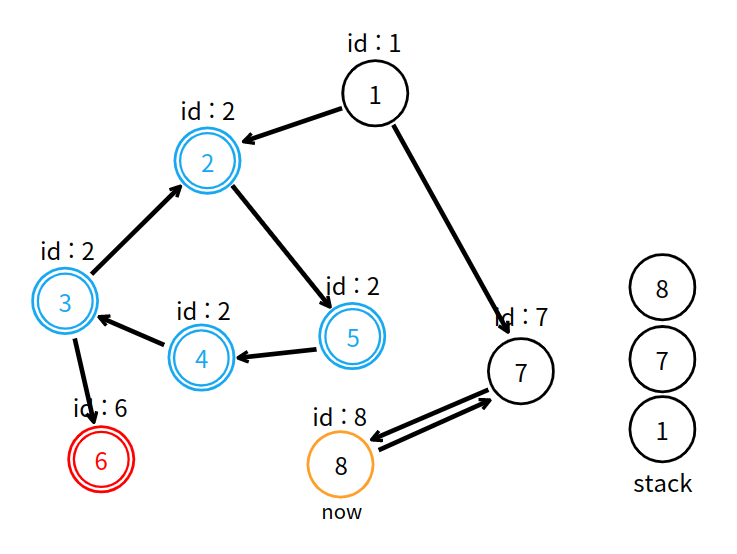
8번 정점에서 이웃 정점을 탐색하던 중, 방문은 했지만 아직 스택에 남아있는 7번 정점을 발견했다. 현재 방문하고 있는 정점의 고유 번호보다 이웃 정점의 고유 번호가 더 작다면, 더 작은 고유 번호로 변환해야하기에, 8번 정점의 고유 번호를 7로 바꾼다.
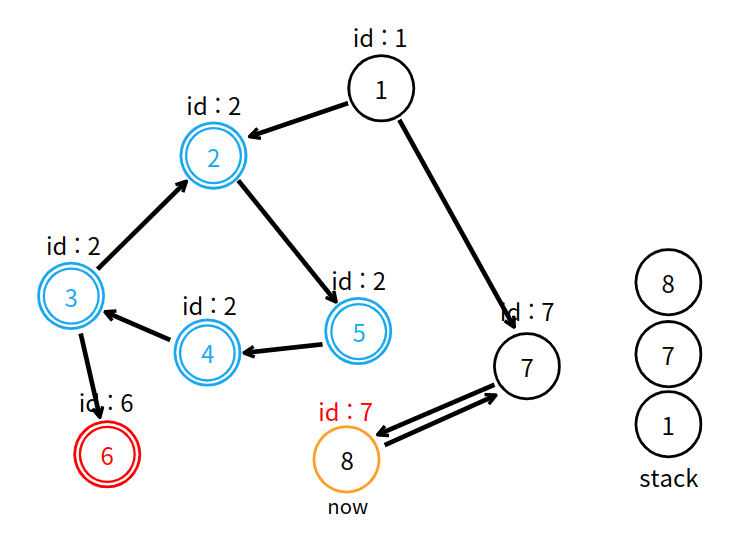
8번 정점의 탐색이 끝났고, 자신이 부여받았던 번호와 고유 번호가 같지 않다. 이전 정점에게 고유 번호를 전달한다.
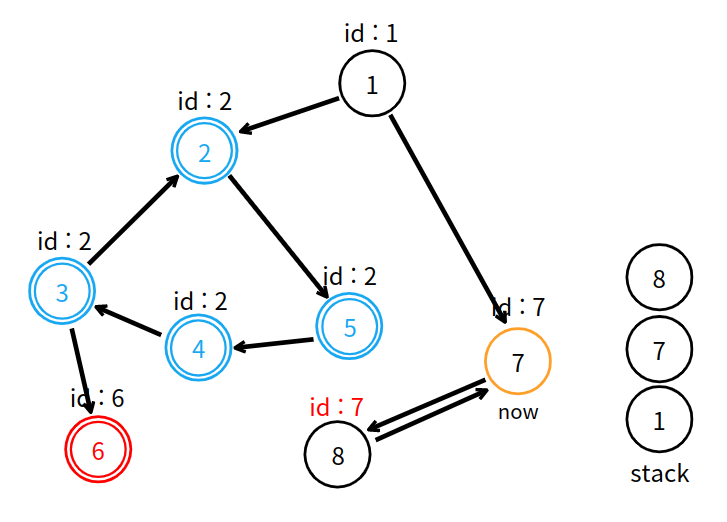
7번 정점의 탐색이 끝났고, 자신이 부여받았던 번호 7은 고유 번호 7과 같으므로 강한 연결 요소로 연결을 시작한다.
현재 쌓여있는 스택에서 자신과 동일한 정점이 나올 때 까지 스택에서 뺀다.
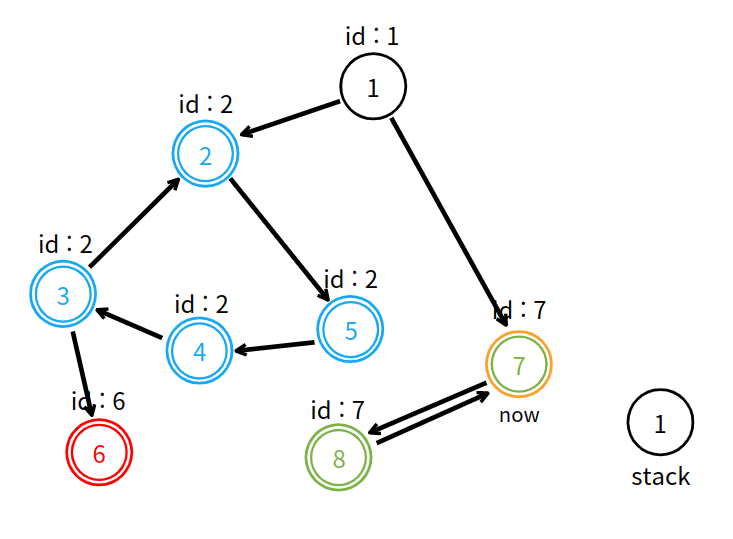
2개의 정점을 가진 강한 연결 요소를 발견했다. 이전 정점에게 고유 번호를 전달한다.
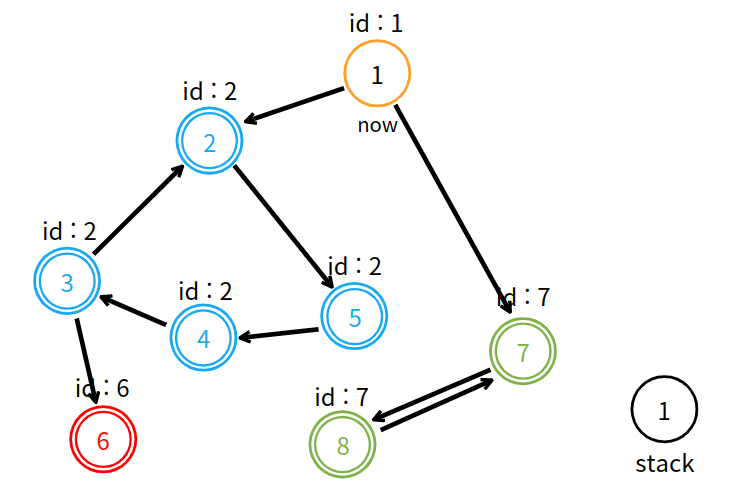
1번 정점의 탐색이 종료됐고, 자신이 부여받았던 번호와 고유 번호가 같으므로 스택에서 자신과 동일한 정점이 나올 때 까지 빼서 강한 연결 요소로 연결한다.
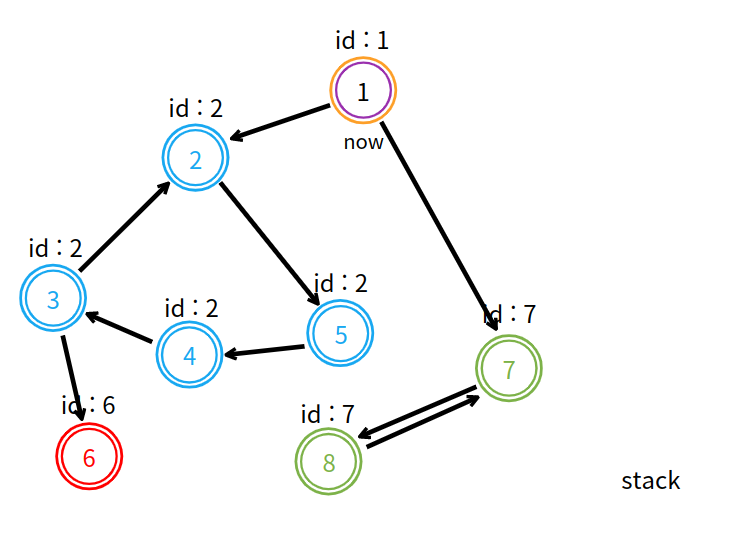
1개 정점을 가진 강한 연결 요소를 발견했다.
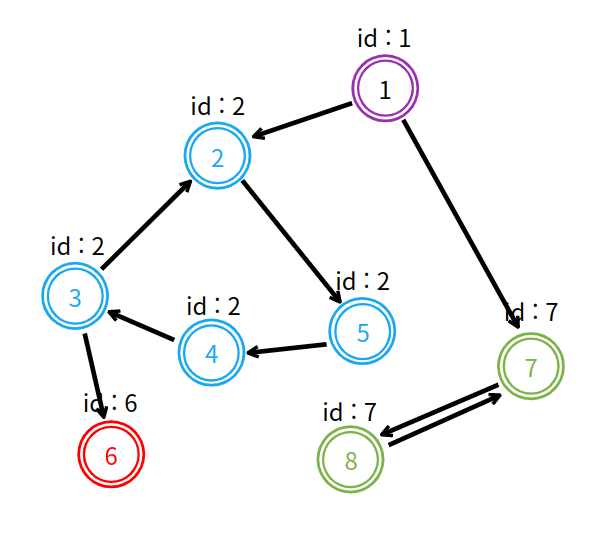
타잔 알고리즘 원리를 이용한 강한 연결 요소 탐색을 완료했다.
코드로 살펴보자.
n = 8 # 정점 개수
graph = [[] for _ in range(n+1)] # 그래프
graph[1] = [2, 7]
graph[2] = [5]
graph[3] = [2, 6]
graph[4] = [3]
graph[5] = [4]
graph[7] = [8]
graph[8] = [7]
id = [0 for _ in range(n+1)] # 정점 고유 번호
cur_id = 1 # 정점 번호
stack = [] # 스택
on_stack = [False for _ in range(n+1)] # 스택에 있는 노드인지 여부
def DFS(i):
global cur_id
id[i] = cur_id # 정점에 고유 번호 부여
cur_id += 1
stack.append(i) # 스택에 쌓기
on_stack[i] = True
parent = id[i]
for next in graph[i]:
if id[next] == 0: # 방문하지 않은 노드는 DFS로 탐색
parent = min(parent, DFS(next))
elif on_stack[next]: # 방문했지만 강한 연결 요소로 묶지 않음
parent = min(parent, id[next]) # 더 작은 고유 번호로 변환
if parent == id[i]: # 사이클 시작점
element = [] # SCC
while stack:
now = stack.pop()
element.append(now)
on_stack[now] = False
if now == i: # 자기 자신 정점이 나올 때 까지 pop
break
print(sorted(element))
id[i] = parent
return parent # 이전 정점에게 고유 번호 전달
for i in range(1, n+1):
if id[i] == 0: # 방문하지 않은 노드 방문
DFS(i)[6]
[2, 3, 4, 5]
[7, 8]
[1]
위에서 설명한 원리를 그대로 코드로 구현했다.
1. DFS로 정점에 방문했다면 정점에 고유 번호를 부여하고, 스택에 쌓기
2. 이웃 정점을 탐색하면서, 방문하지 않은 정점은 DFS로 탐색하고, 방문했지만 강한 연결 요소로 묶지 않은 정점은 고유 번호를 가져와 더 작은 고유 번호로 변환하기
3. 탐색이 끝났다면, 부여받았던 번호와 고유 번호가 같을 때 사이클 시작점으로 판단하고 강한 연결 요소로 스택에 있는 정점들을 자기 자신 정점이 나올 때 까지 묶는다.
4. 이전 정점에게 고유 번호를 전달한다.
코사라주 알고리즘
SCC 를 구현하는 방법 중 DFS 를 두 번 사용하는 알고리즘이다. 증명을 이해하면 직관적인 코드라 쉽게 구현이 가능한 방법이다. 그래프를 순방향으로 DFS 탐색을 한 번 진행한 뒤, 역방향 그래프를 만들어 "순방향 DFS에서 가장 마지막으로 탐색이 끝난 정점부터" DFS 탐색을 한 번 더 진행하면 강한 연결 요소를 얻을 수 있다! 어떻게 이게 가능할까?
탐색이 가장 먼저 끝난 정점은 보통 더 이상 진행할 간선이 없어서 DFS 상으로 제일 먼저 탐색이 종료되지만, 탐색이 가장 마지막으로 끝난 정점은 다른 탐색을 모두 진행한 뒤에 종료되기에 가장 마지막으로 탐색이 끝난다. 그래프를 살펴보자.
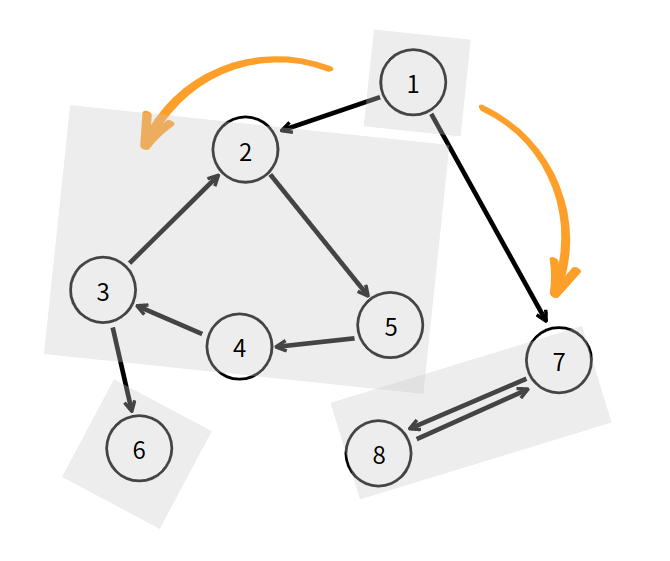
그래프를 눈으로 잘 관찰해보면, 1번부터 8번 정점까지 어느 정점에서 탐색을 시작하던 간에 탐색의 마지막으로 귀결되는 부분이 있고, 탐색의 시작이 되는 부분이 존재한다.
1번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[6, 3, 4, 5, 2, 8, 7, 1]
2번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[6, 3, 4, 5, 2, 8, 7, 1]
3번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[4, 5, 2, 6, 3, 8, 7, 1]
4번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[5, 2, 6, 3, 4, 8, 7, 1]
5번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[2, 6, 3, 4, 5, 8, 7, 1]
6번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[6, 8, 7, 3, 4, 5, 2, 1]
7번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[8, 7, 6, 3, 4, 5, 2, 1]
8번 정점에서 탐색을 시작했을 때의 탐색 종료 순서
[7, 8, 6, 3, 4, 5, 2, 1]
맨 아래에 작성된 코사라주 알고리즘을 구현한 코드를 살짝 수정해서, 특정 정점에서 탐색을 시작했을 때 탐색 종료 순서가 어떻게 달라지는지를 확인해보면, 오른쪽부터 왼쪽으로 갈 수록 그래프의 루트 부분 정점부터 시작해서 리프 부분 정점으로 탐색이 종료된다는 순서가 일정함을 확인할 수 있다.
1번에서 시작했을 때 : 1번 정점 (1번 SCC) -> 7번 정점, 8번 정점 (7번 SCC) -> 2번 정점, 5번 정점, 4번 정점, 3번 정점 (2번 SCC) -> 6번 정점 (6번 SCC)
3번에서 시작했을 때 : 1번 정점 (1번 SCC) -> 7번 정점, 8번 정점 (7번 SCC) -> 3번 정점 (2번 SCC) -> 6번 정점 (6번 SCC) -> 나머지 2번 SCC 정점들
우리는 여기서 역방향 그래프 탐색을 진행할 것이다.
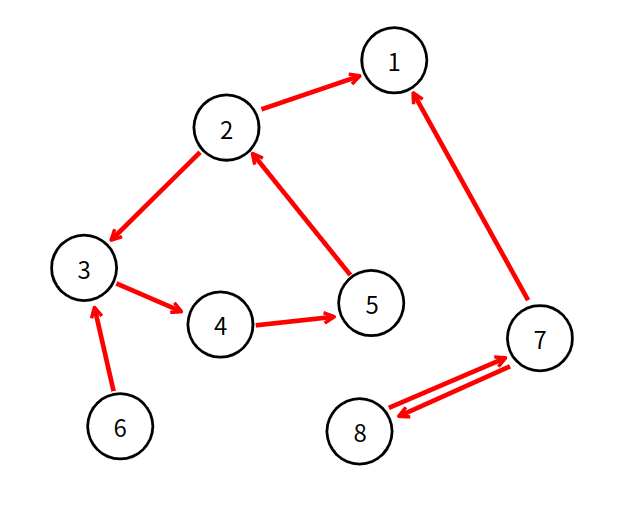
주어진 그래프의 간선 방향을 전부 뒤집어 역방향 그래프를 만들면, 한 가지 관찰을 얻을 수 있는데, 순방향 그래프에서는 모든 탐색을 진행하느라 가장 마지막에 탐색이 종료되었던 1번 정점이 역방향 그래프에선 다른 정점으로 이어지는 간선이 없다는 것이다.
이는 무엇을 의미하냐면, 1번 정점에 DFS 를 진행하면 1번 정점에서만 탐색이 종료되기 때문에 그 자체가 강한 연결 요소가 된다!
1번 정점을 강한 연결 요소로 만든 뒤 7번 정점에 DFS 를 진행하면 7, 8번 정점을 강한 연결 요소로, 2번 정점에 DFS 를 진행하면 2, 3, 4, 5번 정점을 강한 연결 요소로, 마지막으로 6번 정점에 DFS 를 진행하면 6번 정점을 강한 연결 요소로 만들 수 있다.
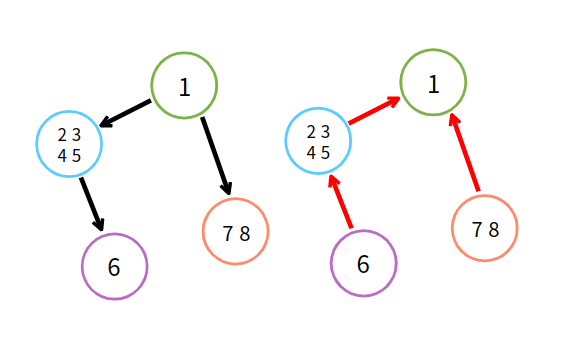
글 초반에 보았던 강한 연결 요소를 하나의 정점으로 만든 그래프를 가져와서 설명을 덧붙이자면, 강한 연결 요소의 정점끼리는 정점 간의 자유로운 이동이 가능하지만, 다른 외부 정점끼리는 기존 간선에서 방향을 바꿔버리면 더이상 그곳으로 향할 수 없기 때문에, 역방향 그래프에서 1번 정점부터 탐색한다는 것은 DFS 가 해당 강한 연결 요소 안에서만 돌다 멈춰버리므로 강한 연결 요소 영역을 구분할 수 있게 만들어준다.
이를 코드로 구현해보자.
n = 8 # 정점 개수
graph = [[] for _ in range(n+1)] # 그래프
graph[1] = [2, 7]
graph[2] = [5]
graph[3] = [2, 6]
graph[4] = [3]
graph[5] = [4]
graph[7] = [8]
graph[8] = [7]
rev_graph = [[] for _ in range(n+1)] # 역방향 그래프
rev_graph[2] = [1, 3]
rev_graph[3] = [4]
rev_graph[4] = [5]
rev_graph[5] = [2]
rev_graph[6] = [3]
rev_graph[7] = [1, 8]
rev_graph[8] = [7]
finished = [] # 탐색이 끝난 노드 순서
visited = [0 for _ in range(n+1)]
def dfs(now): # 순방향 DFS
for next in graph[now]:
if visited[next] == 0:
visited[next] = 1
dfs(next)
finished.append(now)
element = []
def rev_dfs(now): # 역방향 DFS
element.append(now)
for next in rev_graph[now]:
if visited[next] == 0:
visited[next] = 1
rev_dfs(next)
for i in range(1, n+1):
if visited[i] == 0:
visited[i] = 1
dfs(i)
visited = [0 for _ in range(n+1)]
while finished:
cur = finished.pop()
# 탐색이 가장 마지막으로 끝난 그룹의 정점 -> 역방향 그래프에서 가장 첫번째로 끝나는 그룹의 정점
if visited[cur] == 0:
visited[cur] = 1
element = []
rev_dfs(cur)
print(sorted(element))[1]
[7, 8]
[2, 3, 4, 5]
[6]
순방향 DFS와 역방향 DFS 를 구현했다. 순방향 DFS 에서 탐색이 마지막으로 끝난 정점부터 역방향 DFS를 시작함으로써, 강한 연결 요소를 쉽게 구분할 수 있다.
출처
[Tistory] [알고리즘] 강한 연결 요소(1): 코사라주 알고리즘
[알고리즘] 강한 연결 요소(1): 코사라주 알고리즘
강한 연결 요소 (Strongly Connected Component) 시리즈 1. 코사라주 알고리즘 2. 타잔 알고리즘 3. 2-SAT 소개 강한 연결 요소(Strongly Connectioned Component)는 그렇게 잘 알려져 있는 알고리즘이 아니지만 제법
storyofvector7.tistory.com
[Tistory] [알고리즘] 강한 연결 요소(2): 타잔 알고리즘
[알고리즘] 강한 연결 요소(2): 타잔 알고리즘
강한 연결 요소 (Strongly Connected Component) 시리즈 1. 코사라주 알고리즘 2. 타잔 알고리즘 3. 2-SAT 소개 지난 챕터 에서는 코사라주 알고리즘의 소개와 증명에 대해서 설명했습니다. 코사라주 알고리
storyofvector7.tistory.com
[Tistory] [알고리즘/파이썬] 강한 연결 요소 (Strongly Connected Component)
[알고리즘/파이썬] 강한 연결 요소(Strongly Connected Component)
강한 연결 요소란? 강한 연결 요소(SCC)란 노드들이 서로 자유롭게 이동 가능한 모음집이다. 하나의 그래프에서 여러개의 SCC가 존재할 수 있고, 같은 SCC 내에서는 어느 두 노드를 선택하더라도 한
yiyj1030.tistory.com
[Velog] [Algorithm] SCC, Strongly Connected Component 강한연결요소
[Algorithm] SCC, Strongly Connected Component 강한연결요소
개요 SCC란. 보통 유향 그래프안에서 서로 강하게 연결되있는 부분집합을 의미합니다. 여기서 '강하게 연결되있는'이란 하나의 사이클이 형성되는 경우를 뜻하는데, 이런 하나의 SCC내의 두 정점
velog.io
'(예전 글) > 알고리즘 설명' 카테고리의 다른 글
| LCA - 최소 공통 조상 찾기 (0) | 2024.08.16 |
|---|---|
| Sparse Table - 희소 배열 (0) | 2024.08.15 |
| KMP - 문자열 매칭 알고리즘 (0) | 2024.08.15 |