문제
You are given a binary sequence a_1,a_2,…, a_n of length n. You will also be given q queries of two different types.
- : replace with t.
- : Find any satisfying the following conditions, or report that none exists:
- The longest consecutive number of 's in is .
- The longest consecutive number of 's in is .
입력
The first line contains two integers and (1≤n,q≤2×10^5).
The second line contains a binary string of length denoting the binary sequence .
Followed by lines, each is in one of the following formats:
- First type query: (1≤p≤n,t∈{0,1})
- Second type query: (1≤l≤r≤n,0≤x,y≤)
출력
For each query of the second type, if there exists a segment satisfying the conditions, print two integers and separated by a single space. Otherwise, print −1.
If there are multiple possible answers, you may print any.
풀이 과정
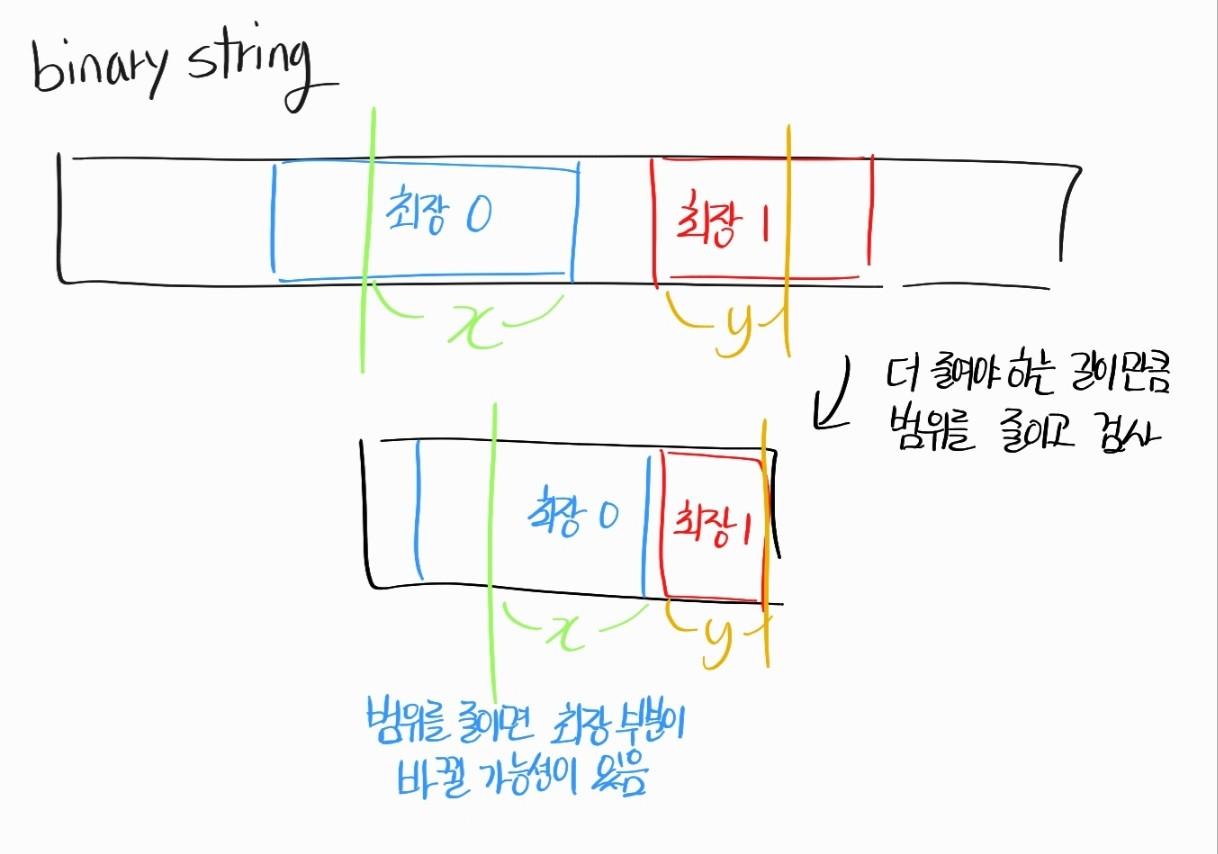
최장 연속 0 부분 길이를 저장하는 금광세그, 최장 연속 1 부분 길이를 저장하는 금광세그를 만들었다. 최장 연속 0 부분 길이가 정확히 x 이고 최장 연속 1 부분 길이가 정확히 y 인 범위를 찾아야 하기 때문에, 최장 연속 0 부분과 최장 연속 1 부분의 시작점과 끝점을 저장했다.
만약 그 구간에서 최장 0 부분 길이가 x보다 작거나 최장 1 부분 길이가 y보다 작다면 그 구간엔 x나 y를 정확히 만족할 수 있는 부분이 없기에 -1을 출력한다.
최장 0 부분 길이가 x와 같고 최장 1 부분 길이가 y와 같을 때 그 구간의 범위를 출력하면 된다.
만약 최장 0 부분 길이가 x보다 같거나 크면서 최장 1 부분 길이가 y보다 같거나 클 때, 최장 0 부분은 (최장 0 부분 길이 - x) 만큼 줄이고, 최장 1 부분은 (최장 1 부분 길이 - y) 만큼 줄여서 x와 y를 정확히 만족할 수 있는 범위를 도출한다.
그러나, 범위를 줄인다면 그 안에 있는 최장 부분이 바뀔 수도 있다. 그렇기 때문에 한번만 줄이는 것이 아니라, 정확히 맞는 x, y의 길이를 가진 최장 부분이 나올 때까지 반복해서 범위를 줄이면 된다.
몰론, 최장 0 부분이 최장 1 부분보다 왼쪽에 있거나 최장 1 부분이 최장 0 부분보다 왼쪽에 있는 두 가지 경우를 고려해서 범위를 줄여가야 한다.
x 가 0이거나 y 가 0 이라면, 그 범위 안에 0이나 1은 절대 들어가면 안되기 때문에, x 가 0이라면 최장 1 부분만 고려하고, y 가 0이라면 최장 0 부분만 고려해서 범위를 잡으면 된다. ( x가 0이거나 y가 0일 땐 만족하는 부분이 없으므로 -1이다. )
#include <stdio.h>
#define SIZE 200005
typedef struct _Node {
int cnt0_left;
int cnt0_left_pos[2];
int cnt0_right;
int cnt0_right_pos[2];
int cnt0_all;
int cnt0_all_pos[2];
int cnt1_left;
int cnt1_left_pos[2];
int cnt1_right;
int cnt1_right_pos[2];
int cnt1_all;
int cnt1_all_pos[2];
int range;
} Node;
char str[SIZE];
Node tree[SIZE * 4];
Node merge(Node a, Node b) {
Node tmp;
// 0 - left
if (a.cnt0_left == a.range && b.cnt0_left != 0) {
tmp.cnt0_left = a.range + b.cnt0_left;
tmp.cnt0_left_pos[0] = a.cnt0_left_pos[0];
tmp.cnt0_left_pos[1] = b.cnt0_left_pos[1];
}
else {
tmp.cnt0_left = a.cnt0_left;
tmp.cnt0_left_pos[0] = a.cnt0_left_pos[0];
tmp.cnt0_left_pos[1] = a.cnt0_left_pos[1];
}
// 0 - right
if (b.cnt0_right == b.range && a.cnt0_right != 0) {
tmp.cnt0_right = a.cnt0_right + b.range;
tmp.cnt0_right_pos[0] = a.cnt0_right_pos[0];
tmp.cnt0_right_pos[1] = b.cnt0_right_pos[1];
}
else {
tmp.cnt0_right = b.cnt0_right;
tmp.cnt0_right_pos[0] = b.cnt0_right_pos[0];
tmp.cnt0_right_pos[1] = b.cnt0_right_pos[1];
}
// 0 - all
if (a.cnt0_all >= b.cnt0_all && a.cnt0_all >= a.cnt0_right + b.cnt0_left) {
tmp.cnt0_all = a.cnt0_all;
tmp.cnt0_all_pos[0] = a.cnt0_all_pos[0];
tmp.cnt0_all_pos[1] = a.cnt0_all_pos[1];
}
else if (b.cnt0_all >= a.cnt0_all && b.cnt0_all >= a.cnt0_right + b.cnt0_left) {
tmp.cnt0_all = b.cnt0_all;
tmp.cnt0_all_pos[0] = b.cnt0_all_pos[0];
tmp.cnt0_all_pos[1] = b.cnt0_all_pos[1];
}
else { // (a.cnt0_right + b.cnt0_left >= a.cnt0_all && a.cnt0_right + b.cnt0_left >= b.cnt0_all)
tmp.cnt0_all = a.cnt0_right + b.cnt0_left;
if (a.cnt0_right == 0 || b.cnt0_left == 0) {
if (a.cnt0_right == 0 && b.cnt0_left == 0) {
// ...?
tmp.cnt0_all_pos[0] = a.cnt0_right_pos[0];
tmp.cnt0_all_pos[1] = b.cnt0_left_pos[1];
}
else if (a.cnt0_right == 0) {
tmp.cnt0_all_pos[0] = b.cnt0_left_pos[0];
tmp.cnt0_all_pos[1] = b.cnt0_left_pos[1];
}
else if (b.cnt0_left == 0) {
tmp.cnt0_all_pos[0] = a.cnt0_right_pos[0];
tmp.cnt0_all_pos[1] = a.cnt0_right_pos[1];
}
}
else {
tmp.cnt0_all_pos[0] = a.cnt0_right_pos[0];
tmp.cnt0_all_pos[1] = b.cnt0_left_pos[1];
}
}
// 1 - left
if (a.cnt1_left == a.range && b.cnt1_left != 0) {
tmp.cnt1_left = a.range + b.cnt1_left;
tmp.cnt1_left_pos[0] = a.cnt1_left_pos[0];
tmp.cnt1_left_pos[1] = b.cnt1_left_pos[1];
}
else {
tmp.cnt1_left = a.cnt1_left;
tmp.cnt1_left_pos[0] = a.cnt1_left_pos[0];
tmp.cnt1_left_pos[1] = a.cnt1_left_pos[1];
}
// 1 - right
if (b.cnt1_right == b.range && a.cnt1_right != 0) {
tmp.cnt1_right = a.cnt1_right + b.range;
tmp.cnt1_right_pos[0] = a.cnt1_right_pos[0];
tmp.cnt1_right_pos[1] = b.cnt1_right_pos[1];
}
else {
tmp.cnt1_right = b.cnt1_right;
tmp.cnt1_right_pos[0] = b.cnt1_right_pos[0];
tmp.cnt1_right_pos[1] = b.cnt1_right_pos[1];
}
// 1 - all
if (a.cnt1_all >= b.cnt1_all && a.cnt1_all >= a.cnt1_right + b.cnt1_left) {
tmp.cnt1_all = a.cnt1_all;
tmp.cnt1_all_pos[0] = a.cnt1_all_pos[0];
tmp.cnt1_all_pos[1] = a.cnt1_all_pos[1];
}
else if (b.cnt1_all >= a.cnt1_all && b.cnt1_all >= a.cnt1_right + b.cnt1_left) {
tmp.cnt1_all = b.cnt1_all;
tmp.cnt1_all_pos[0] = b.cnt1_all_pos[0];
tmp.cnt1_all_pos[1] = b.cnt1_all_pos[1];
}
else { // (a.cnt0_right + b.cnt0_left >= a.cnt0_all && a.cnt0_right + b.cnt0_left >= b.cnt0_all)
tmp.cnt1_all = a.cnt1_right + b.cnt1_left;
if (a.cnt1_right == 0 || b.cnt1_left == 0) {
if (a.cnt1_right == 0 && b.cnt1_left == 0) {
// ...?
tmp.cnt1_all_pos[0] = a.cnt1_right_pos[0];
tmp.cnt1_all_pos[1] = b.cnt1_left_pos[1];
}
else if (a.cnt1_right == 0) {
tmp.cnt1_all_pos[0] = b.cnt1_left_pos[0];
tmp.cnt1_all_pos[1] = b.cnt1_left_pos[1];
}
else if (b.cnt1_left == 0) {
tmp.cnt1_all_pos[0] = a.cnt1_right_pos[0];
tmp.cnt1_all_pos[1] = a.cnt1_right_pos[1];
}
}
else {
tmp.cnt1_all_pos[0] = a.cnt1_right_pos[0];
tmp.cnt1_all_pos[1] = b.cnt1_left_pos[1];
}
}
tmp.range = a.range + b.range;
return tmp;
}
void bitset(int start, int end, int idx, char val) {
if (val == '0') {
tree[idx].cnt0_left = 1;
tree[idx].cnt0_left_pos[0] = start;
tree[idx].cnt0_left_pos[1] = end;
tree[idx].cnt0_right = 1;
tree[idx].cnt0_right_pos[0] = start;
tree[idx].cnt0_right_pos[1] = end;
tree[idx].cnt0_all = 1;
tree[idx].cnt0_all_pos[0] = start;
tree[idx].cnt0_all_pos[1] = end;
tree[idx].cnt1_left = 0;
tree[idx].cnt1_left_pos[0] = start;
tree[idx].cnt1_left_pos[1] = end;
tree[idx].cnt1_right = 0;
tree[idx].cnt1_right_pos[0] = start;
tree[idx].cnt1_right_pos[1] = end;
tree[idx].cnt1_all = 0;
tree[idx].cnt1_all_pos[0] = start;
tree[idx].cnt1_all_pos[1] = end;
tree[idx].range = 1;
}
else {
tree[idx].cnt0_left = 0;
tree[idx].cnt0_left_pos[0] = start;
tree[idx].cnt0_left_pos[1] = end;
tree[idx].cnt0_right = 0;
tree[idx].cnt0_right_pos[0] = start;
tree[idx].cnt0_right_pos[1] = end;
tree[idx].cnt0_all = 0;
tree[idx].cnt0_all_pos[0] = start;
tree[idx].cnt0_all_pos[1] = end;
tree[idx].cnt1_left = 1;
tree[idx].cnt1_left_pos[0] = start;
tree[idx].cnt1_left_pos[1] = end;
tree[idx].cnt1_right = 1;
tree[idx].cnt1_right_pos[0] = start;
tree[idx].cnt1_right_pos[1] = end;
tree[idx].cnt1_all = 1;
tree[idx].cnt1_all_pos[0] = start;
tree[idx].cnt1_all_pos[1] = end;
tree[idx].range = 1;
}
}
void init(int start, int end, int idx) {
if (start == end) {
bitset(start, end, idx, str[start]);
return;
}
int mid = (start + end) / 2;
init(start, mid, idx * 2);
init(mid + 1, end, idx * 2 + 1);
tree[idx] = merge(tree[idx * 2], tree[idx * 2 + 1]);
}
void update(int start, int end, int idx, int what, int value) {
if (what < start || end < what) return;
if (start == end) {
bitset(start, end, idx, value + '0');
return;
}
int mid = (start + end) / 2;
update(start, mid, idx * 2, what, value);
update(mid + 1, end, idx * 2 + 1, what, value);
tree[idx] = merge(tree[idx * 2], tree[idx * 2 + 1]);
}
Node interval(int start, int end, int idx, int left, int right) {
Node tmp;
tmp.cnt0_left = 0; tmp.cnt0_left_pos[0] = start; tmp.cnt0_left_pos[1] = end;
tmp.cnt0_right = 0; tmp.cnt0_right_pos[0] = start; tmp.cnt0_right_pos[1] = end;
tmp.cnt0_all = 0; tmp.cnt0_all_pos[0] = start; tmp.cnt0_all_pos[1] = end;
tmp.cnt1_left = 0; tmp.cnt1_left_pos[0] = start; tmp.cnt1_left_pos[1] = end;
tmp.cnt1_right = 0; tmp.cnt1_right_pos[0] = start; tmp.cnt1_right_pos[1] = end;
tmp.cnt1_all = 0; tmp.cnt1_all_pos[0] = start; tmp.cnt1_all_pos[1] = end;
tmp.range = end - start + 1;
if (end < left || right < start) return tmp;
if (left <= start && end <= right) return tree[idx];
int mid = (start + end) / 2;
return merge(interval(start, mid, idx * 2, left, right), interval(mid + 1, end, idx * 2 + 1, left, right));
}
int main(void) {
int n, q;
scanf("%d %d", &n, &q);
scanf("%s", str);
init(0, n - 1, 1);
for (int i = 0; i < q; i++) {
int mode;
scanf("%d", &mode);
if (mode == 1) {
int p, t;
scanf("%d %d", &p, &t);
update(0, n - 1, 1, p - 1, t);
}
else {
int l, r, x, y;
scanf("%d %d %d %d", &l, &r, &x, &y);
Node result;
while (1) {
if (l > r || (x == 0 && y == 0)) {
printf("-1\n");
break;
}
result = interval(0, n - 1, 1, l - 1, r - 1);
int max0_cnt;
int max0_pos[2];
int max1_cnt;
int max1_pos[2];
if (result.cnt0_left >= result.cnt0_right && result.cnt0_left >= result.cnt0_all) {
max0_cnt = result.cnt0_left;
max0_pos[0] = result.cnt0_left_pos[0];
max0_pos[1] = result.cnt0_left_pos[1];
}
else if (result.cnt0_right >= result.cnt0_left && result.cnt0_right >= result.cnt0_all) {
max0_cnt = result.cnt0_right;
max0_pos[0] = result.cnt0_right_pos[0];
max0_pos[1] = result.cnt0_right_pos[1];
}
else {
max0_cnt = result.cnt0_all;
max0_pos[0] = result.cnt0_all_pos[0];
max0_pos[1] = result.cnt0_all_pos[1];
}
if (result.cnt1_left >= result.cnt1_right && result.cnt1_left >= result.cnt1_all) {
max1_cnt = result.cnt1_left;
max1_pos[0] = result.cnt1_left_pos[0];
max1_pos[1] = result.cnt1_left_pos[1];
}
else if (result.cnt1_right >= result.cnt1_left && result.cnt1_right >= result.cnt1_all) {
max1_cnt = result.cnt1_right;
max1_pos[0] = result.cnt1_right_pos[0];
max1_pos[1] = result.cnt1_right_pos[1];
}
else {
max1_cnt = result.cnt1_all;
max1_pos[0] = result.cnt1_all_pos[0];
max1_pos[1] = result.cnt1_all_pos[1];
}
//printf("(%d-%d) Max0 %lld (%d-%d) Max1 %lld (%d-%d)\n",l, r, max0_cnt, max0_pos[0], max0_pos[1], max1_cnt, max1_pos[0], max1_pos[1]);
if (max0_cnt < x || max1_cnt < y) {
printf("-1\n");
break;
}
else if (max0_cnt == x && max1_cnt == y) {
printf("%d %d\n", l, r);
break;
}
else {
// left - right relation check
if (max0_pos[1] < max1_pos[0]) { // 0 - 1
if (x != 0) l = max0_pos[0] + 1 + (max0_cnt - x);
else l = max1_pos[0] + 1;
if (y != 0) r = max1_pos[1] + 1 - (max1_cnt - y);
else r = max0_pos[1] + 1;
}
else { // 1 - 0
if (y != 0) l = max1_pos[0] + 1 + (max1_cnt - y);
else l = max0_pos[0] + 1;
if (x != 0) r = max0_pos[1] + 1 - (max0_cnt - x);
else r = max1_pos[1] + 1;
}
}
}
}
}
return 0;
}'-- 예전 기록 > BOJ' 카테고리의 다른 글
| [ BOJ ] 2557 : Hello World ( BRONZE 5 ) / C, C++, Python, Java (0) | 2023.05.29 |
|---|---|
| [ BOJ ] 21039 : Flip and Combos ( DIAMOND 5 ) / C (0) | 2023.05.29 |
| [ BOJ ] 18407 : 가로 블록 쌓기 ( PLATINUM 3 ) / C (2) | 2023.05.28 |
| [ BOJ ] 3002 : 아날로그 다이얼 ( PLATINUM 2 ) / C (0) | 2023.05.01 |
| [ BOJ ] 9345 : 디지털 비디오 디스크(DVDs) ( PLATINUM 3 ) / C (0) | 2023.04.18 |