
문제 링크 : https://www.acmicpc.net/problem/10423
풀이 과정
목표는 모든 도시를 발전소가 설치된 도시와 연결하는 것, 연결할 때 케이블을 최소 비용으로 설치하는 것이다. 도시를 최소 비용으로 연결하기 위해 최소 스패닝 트리 알고리즘을 사용하지만, 모든 도시가 발전소와 단순히 "연결"되어 있기만 하면 되므로 이 알고리즘을 살짝 변형시켜주면 된다.
1. 크루스칼 알고리즘 변형하기
먼저, 기본 크루스칼 알고리즘의 전체적인 실행 순서에 대해 알아보자.
- n개의 노드가 있을 때, m개의 간선들을 비용 기준으로 오름차순 정렬한다.
- 정렬된 간선들을 차례대로 순회하면서, 간선이 연결하는 두 노드가 다른 부모 노드를 바라볼 때 (그룹이 다를 때) 두 노드를 연결한다.
- 2번으로 n - 1 개의 간선을 연결했다면 종료한다. (n개의 노드는 최소 n - 1 개의 간선으로 연결할 수 있다.)
위 과정을 수행하면, n 개의 노드가 최소 비용으로 연결된다.
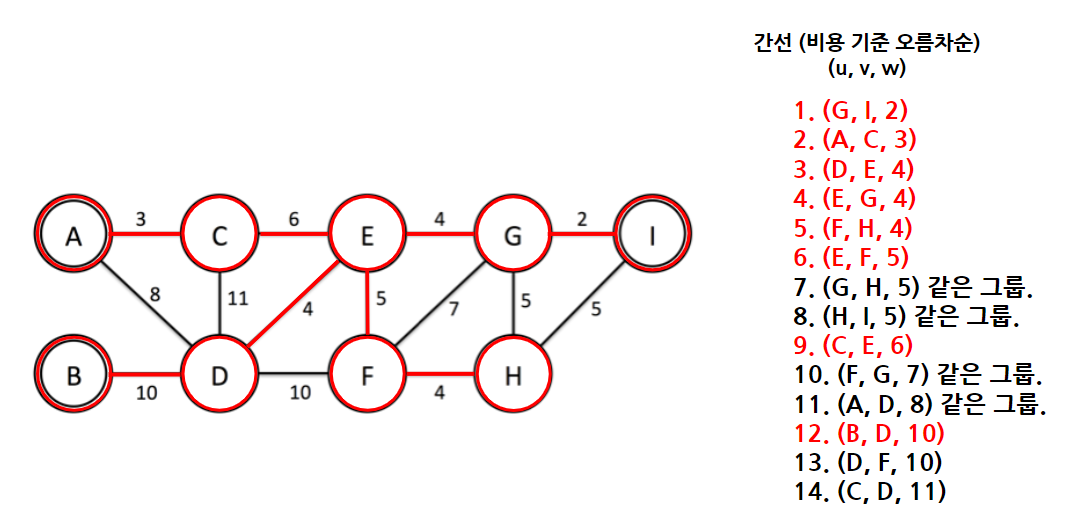
이 문제에 해당 과정을 적용하면 다음과 같은 방식으로 연결된다.

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | C | D | E | F | G | H | I |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | C | D | E | F | G | H | G |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | A | D | E | F | G | H | G |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | A | D | D | F | G | H | G |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | A | G | G | F | G | H | G |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | A | G | G | F | G | F | G |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | A | B | A | G | G | G | G | G | G |

| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | G | B | G | G | G | G | G | G | G |
| 노드 | A | B | C | D | E | F | G | H | I |
| 부모 | G | G | G | G | G | G | G | G | G |
9개의 정점을 최소 비용인 8개의 간선으로 이었다.
같은 그룹인지에 대한 판단은, 각 노드가 가리키는 부모 노드 배열로 판단한다. 두 노드가 같은 부모 노드를 가리킨다면 같은 그룹이다. (처음엔 부모 노드로 자기 자신 노드를 가리키다가, 다른 그룹에 이어졌다면 해당 그룹을 부모 노드로 가리킨다.)
2. 발전소에만 연결하면 된다
위의 실행 과정은, 이 문제에서의 답이 되지 않는다.
다음 포인트를 이용해 위 알고리즘을 변형해보자.
1. 모든 노드를 굳이 연결하지 않아도 되고, 발전소랑만 연결되면 된다.
2. 편의를 위해, 한 그룹에서의 노드들이 그 그룹에 연결된 발전소를 부모 노드로 바라보도록 한다. 그러면 해당 노드의 부모 노드가 발전소인지 아닌지 여부에 따라, 그 노드가 발전소와 연결되었는지 여부를 확인할 수 있다.
3. 알고리즘을 수행하면서, 연결하고자 하는 두 그룹이 모두 발전소와 연결되었다면 (두 노드 모두 부모 노드가 발전소라면), 연결하지 않는다.
4. 3번으로 인해 간선을 더 건너뛰므로, 또 다른 연결할 수 있는 간선을 찾기 위해 m 개의 간선 전체를 순회한다.
이렇게 변형해서 수행하면, 다음과 같이 바뀐다.
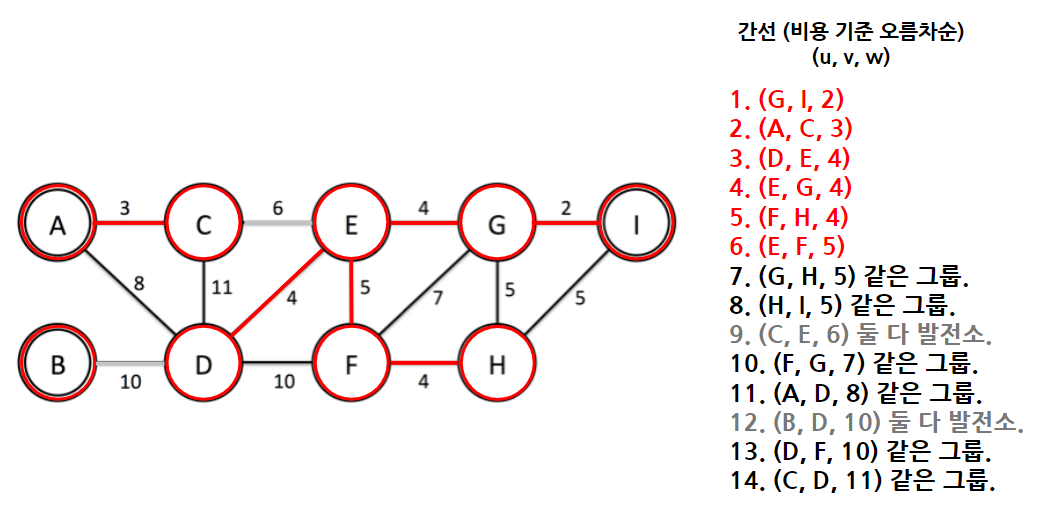
전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
import java.util.Arrays;
import java.util.Stack;
class Edge {
int u, v, w;
public Edge(int u, int v, int w) {
this.u = u;
this.v = v;
this.w = w;
}
}
class MinnimumSpanningTree {
private int n, m;
private int[] power_station; // 발전소 여부
private Edge[] edges; // 간선 배열
private int[] parent; // 부모 노드 배열
public MinnimumSpanningTree(int n, int m) {
this.n = n;
this.m = m;
edges = new Edge[m];
power_station = new int[n+1];
Arrays.fill(power_station, 0);
parent = new int[n+1];
for (int i = 1; i <= n; i++) parent[i] = i;
}
public void addPowerStation(int p) { power_station[p] = 1; }
public void addEdge(int i, int u, int v, int w) { edges[i] = new Edge(u, v, w); }
public void sortEdges() {
// Kruskal : 간선 정렬
Arrays.sort(edges, (e1, e2) -> Integer.compare(e1.w, e2.w));
}
public boolean isPower(int a) {
// power_station[a] == 1 쓰기가 귀찮아서..
if (power_station[a] == 1) return true;
return false;
}
public int find(int a) {
// Union Find : 부모 노드를 스택으로 찾으며, 나머지 노드 모두 부모를 동기화하는 함수
Stack<Integer> citys = new Stack<>();
while (a != parent[a]) {
citys.push(a);
a = parent[a];
}
while (!citys.isEmpty()) {
parent[citys.peek()] = a;
citys.pop();
}
return a;
}
public void union(int a, int b) {
// Union Find : a와 b 를 같은 그룹으로 잇는 함수
a = find(a);
b = find(b);
// 발전기가 있는 그룹에 잇는다.
if (isPower(a)) parent[b] = a;
else parent[a] = b;
}
public int solve() {
// Kruskal : 비용이 적은 노드부터 그룹을 잇는다.
sortEdges();
int result = 0;
for (int i = 0; i < m; i++) {
int now_a = find(edges[i].u);
int now_b = find(edges[i].v);
if (isPower(now_a) && isPower(now_b)) continue;
if (now_a != now_b) {
union(now_a, now_b);
result += edges[i].w;
}
}
return result;
}
}
class Main {
static public void main(String []args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 도시의 개수
int m = Integer.parseInt(st.nextToken()); // 설치 가능한 케이블의 수
int k = Integer.parseInt(st.nextToken()); // 발전소의 개수
// 최소 스패닝 트리 Class 생성
MinnimumSpanningTree mst = new MinnimumSpanningTree(n, m);
st = new StringTokenizer(br.readLine());
// 발전소 정보 등록하기
for (int i = 0; i < k; i++) mst.addPowerStation(Integer.parseInt(st.nextToken()));
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
// 간선 정보 등록하기
mst.addEdge(i, u, v, w);
}
// 최소 스패닝 트리를 만들며, 만약 이미 발전소랑 이어진 그룹이라면 잇지 않는다.
System.out.println(mst.solve());
}
}'알고리즘 문제 풀이 > 백준 문제 풀이' 카테고리의 다른 글
| 백준 1477 - 휴게소 세우기 (1) | 2024.11.15 |
|---|---|
| 백준 5214 - 환승 (0) | 2024.11.08 |
| 백준 24520 - Meet In The Middle (0) | 2024.08.16 |
| 백준 13511 - 트리와 쿼리 2 (0) | 2024.08.16 |
| 백준 3176 - 도로 네트워크 (0) | 2024.08.16 |