[ 확률통계 ] 표본분산을 구할 때 n-1로 나누는 이유

어떤 모집단에서 조사하고자 하는 특성을 나타내는 확률변수를 X라고 할 때, X의 평균, 분산, 표준편차를 모평균, 모분산, 모표준편차라고 한다. 

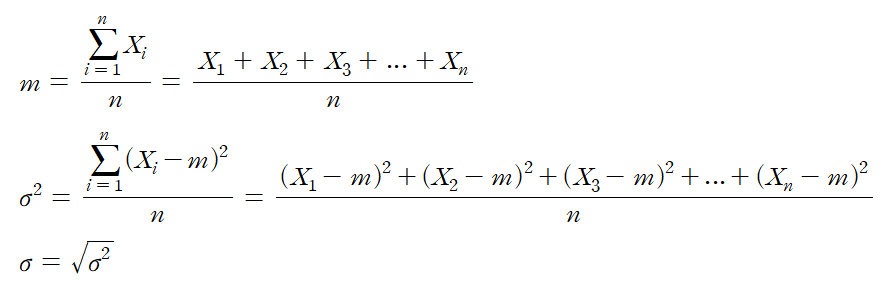
모집단에서 임의추출한 크기가 n인 표본을

이라 할 때, 이들의 평균, 분산, 표준편차를 표본평균, 표본분산, 표본표준편차라고 부른다.

 

 

 

 

표본분산을 계산할 때, n이 아니라 n-1로 나누는 이유는?

분산은 평균과의 차를 제곱한 것들의 합을 n으로 나누어 계산한다. 모집단의 분산을 구하기 위해서는 모집단의 평균과의 차를 제곱한 것들의 합을 n으로 나누어 계산하면 되지만, 모집단이 너무 크다면 모평균과 모분산을 구하기 힘들다. (데이터 수가 많기 때문에) 그렇기에 모집단에서 추출한 표본을 이용해 표본평균과 표본분산을 구하여 모분산을 추정하려고 한다. 

그런데 모집단에서 추출한 표본이 모분산을 잘 측정해주는 데이터가 안 나올 가능성이 존재한다..

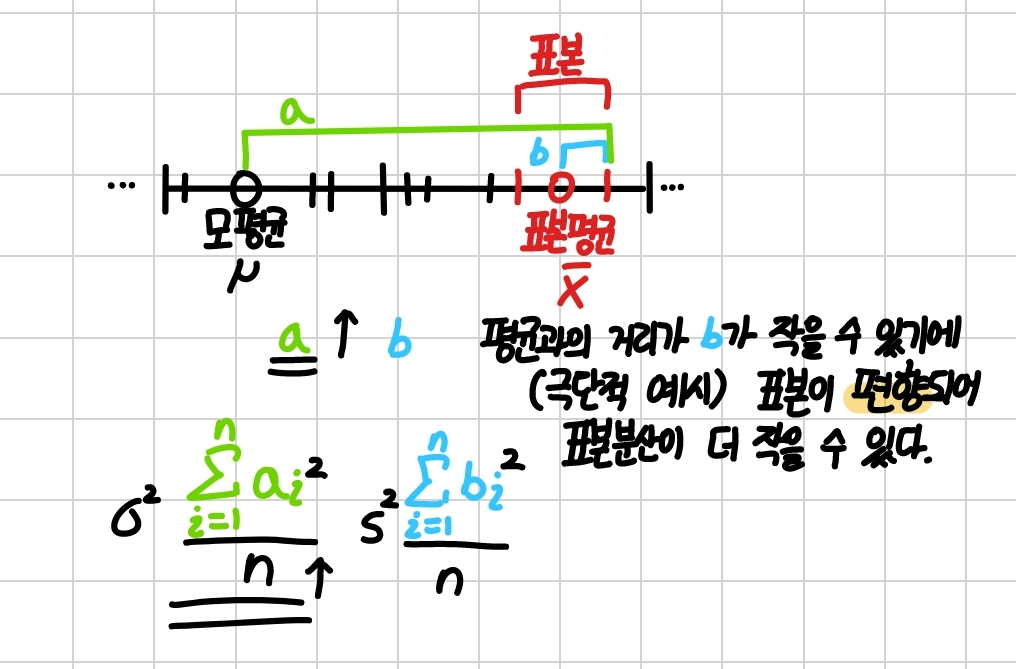
평균과의 거리 제곱의 합이 표본분산 쪽이 더 작아질 가능성이 있기에, 이를 모분산과 비슷하게 측정하기 위하여 표본분산의 분자 뿐만 아니라 표본분산의 분모 또한 작게 만들어주어야 한다. 여기에서 n이 아니라 n-1으로 나눠준다면, 모분산을 정확하게는 아니더라도 어느 정도 맞게 측정할 수 있다. 이렇게 표본에서 구한 어떤 통계랑의 기댓값이 모수와 같을 때의 통계량을 불편추정량이라고 한다. ( n으로 나눈다면 편의추정량이라고 한다. )

 

n-1로 나누는 것이 맞음을 증명해보자.

데이터 표본들의 분산을 모두 구한 뒤, 그 분산들을 전부 모아 평균값을 도출하면 모집단 데이터의 분산과 같다.

1, 3, 5 의 모분산은 8/3이며, 데이터의 표본 경우의 수를 구하고 그에 대한 표본분산을 다 구하여 표본분산의 평균값을 계산하였다.

데이터의 표본을 모두 구해서 표본분산 공식을 이용해 ( 평균과의 거리 제곱들의 합을 n - 1로 나눔 ) 모든 표본들의 표본분산을 구하고, 표본분산의 기댓값 (평균) 을 구하면 모분산과 같다는 것을 알 수 있다.

증명

증명하기 전에, 몇 가지 정의를 소개하고 시작한다.

먼저, 표본분산의 기댓값이 모분산이라는 것을 증명할 것이다.

이와 같이 표본분산을 계산할 때 n-1로 나눠서 계산한다면 표본분산의 기댓값이 모분산이 되기에 옳다.

(+) 표본평균의 분산이 모분산 / n 인 이유는 무엇일까?

이를 통해 모분산은 표본을 추출해 분산을 구했을 때의 평균과 같음으로써, 표본분산을 계산할 때 n이 아닌 n-1로 나누는 것이 모분산과 비슷한 값을 추정해낼 수 있음을 생각할 수 있다.