
도입
이 글은 자료구조에서 스택 다음으로 배우게 되는 큐에 대한 개념을 담고 있습니다. 스택과 유사하지만 다른 특징을 가지고 있으며, 큐 자료 구조에 대한 기반을 다져 놓으면 실전적으로 활용이 가능합니다. 큐는 다른 수많은 알고리즘 (BFS, 위상 정렬, 데이크스트라 등등) 을 배우는 데에 있어서 필수적인 기초가 되는 알고리즘이기 때문에, 큐의 개념을 이해하고 여러 문제에 활용하며 풀이한 뒤, 추후 적극적으로 응용이 가능하도록 능력을 기르는 것이 이 글의 목적입니다.
본 글은 C를 기반으로 작성되었습니다.
스택 자료 구조를 먼저 공부한 이후 큐를 공부하는 것을 추천드립니다. https://readytojoin.tistory.com/35
스택 (Stack)
스택 (Stack) 은 한 쪽 끝에서만 데이터를 넣거나 뺄 수 있는 자료 구조이다. 제일 마지막에 넣는 것이 먼저 나온다는 LIFO ( Last In First Out ) 특성을 가지고 있다. 데이터를 입력된 순서대로 저장하고
readytojoin.tistory.com
접근
https://www.acmicpc.net/problem/10845
10845번: 큐
첫째 줄에 주어지는 명령의 수 N (1 ≤ N ≤ 10,000)이 주어진다. 둘째 줄부터 N개의 줄에는 명령이 하나씩 주어진다. 주어지는 정수는 1보다 크거나 같고, 100,000보다 작거나 같다. 문제에 나와있지
www.acmicpc.net
스택과는 다른 자료 구조인 큐를 사용하는 문제가 등장한다. 큐는 어떤 상황에서 사용할 수 있을까?
데이터 순차 처리

큐 (queue) 는 기다리는 줄, 대기 행렬 등의 뜻을 가지고 있다. 기다리는 행렬이 있고 하나 둘씩 요청을 처리하는 것처럼 주로 들어오는 순서대로 명령을 처리할 때 사용되는 자료 구조가 큐이다.

들어오는 순서대로 명령을 처리한다는 것은 어떻게 보면 프로그래밍에서는 당연한 이야기(...)라서 잘 이해가 되지 않을 수도 있다. 큐의 원리는 일상생활에서 많이 사용되고 있다. 음악 재생 프로그램에서 곡의 대기열을 Queue 라고 부르기도 하는 등 여러 분야에서 사용된다.
추가한 음악을 차례대로 재생하는 것처럼, 들어온 데이터를 차례대로 저장하는 데에 큐가 사용된다. 그런데 우리는 들어온 데이터를 저장해 두는 스택을 배웠기에 별 차이점이 없는 것처럼 느껴질 것이다.
스택 구조와 다른 점은 바로 데이터를 꺼내는 곳이 다르다는 차이점이 있다!
다음과 같은 문제를 예시로 들어보자.

본래 스택은 가장 먼저 들어온 데이터를 깊숙이 저장하고, 가장 마지막에 들어온 데이터를 먼저 빼낼 수 있는 구조였기에, 이 문제는 가장 먼저 들어온 사람이 버스에서 하차하기에 스택을 사용할 수 없다.
이것 또한 그냥 구현이 가능한 문제지만 큐 자료 구조를 배운 후 적용해보자.
큐 ( Queue )
큐는 한 쪽 끝에 데이터를 넣고 다른 한 쪽 끝에서 데이터를 뺄 수 있는 자료 구조이다. 가장 먼저 들어온 데이터가 가장 먼저 나간다는 특징 ( FIFO, First-In First-Out ) 을 가지고 있다. 주로 일렬로 들어오는 데이터를 들어오는 순서대로 처리하는 데에 사용되는 자료 구조이다.

큐에 데이터가 쌓이는 구조이다. 데이터가 추가되는 과정은 스택과 동일하다. 그러나 데이터를 뺄 때는 제일 먼저 넣은 ( 제일 깊숙히 넣은 데이터부터 ) 뺀다.
원래 스택에서는 Top 을 이용해 데이터 추가, 삭제 등을 관리했지만, 큐에서 제일 깊숙히 넣은 데이터를 삭제하는 행위를 관리하기 위해 Rear 라는 변수를 사용한다.
Top 변수에서 가장 높은 곳에 쌓인 데이터의 위치를 알려주는 것처럼, Rear 변수는 가장 낮은 곳에 쌓인 데이터의 위치를 알려준다. 이를 이용해 큐에 데이터를 추가할 땐 Top 변수를, 큐에서 데이터를 삭제할 땐 Rear 변수를 이용해 관리하는 것이 가능하다.
큐 구조 이해

프로그램을 시작하고 큐를 새로 만들면 아무런 데이터도 쌓여있지 않기 때문에 큐는 비어있고 Top과 Rear 변수는 -1의 값을 가지고 있다. 비어있는 큐에 3이라는 데이터를 넣어보자.

데이터를 추가하는 과정은 스택과 동일하다. Top 변수를 이용해 큐에 데이터를 계속해서 추가할 수 있다.
큐가 비어있는 중에 데이터가 들어온다면 -1 값을 가지고 있던 Rear 변수는 데이터의 가장 낮은 곳을 가리킨다.
Rear 값을 이용한 데이터 삭제 과정을 살펴보자.
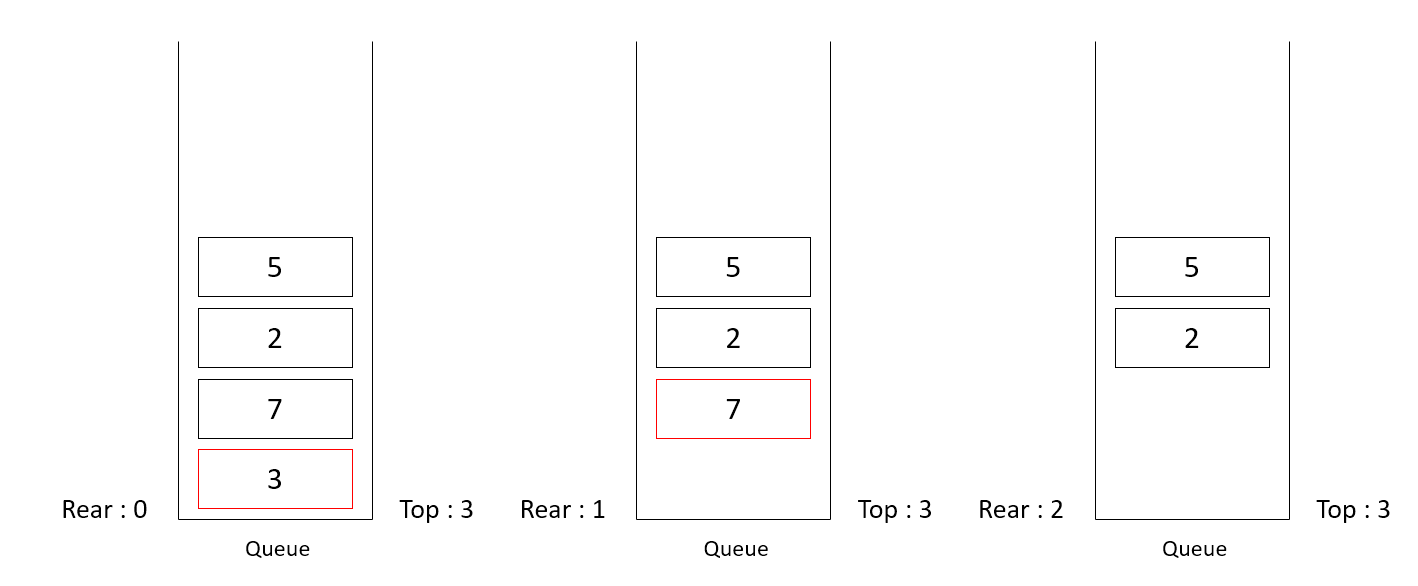
스택에서는 제일 나중에 들어온 데이터를 먼저 꺼내기에 Top 값을 이용했다면, 큐에서는 제일 먼저 들어온 데이터를 먼저 꺼내기에 Rear 값을 증가시키며 데이터를 꺼낼 수 있다.
큐 - Enqueue
스택과는 달리, 큐에 데이터를 넣는 것을 Enqueue라고 한다. 단순 데이터를 넣는 행위이기 때문에 마찬가지로 O(1)의 시간복잡도를 가진다.

현재 큐의 Top이 2이기 때문에, 2번째 데이터보다 위인 3번째 데이터로 넣고 싶은 데이터를 Enqueue 한다.
Enqueue를 코드로 구현하면 다음과 같다.
int queue[SIZE];
int top = -1;
int rear = -1;
void enqueue(int x) {
if (rear == -1)
rear = 0;
queue[++top] = x;
}스택에 데이터를 push하는 과정과 유사하지만, Rear 값을 관리해야 한다.
맨 처음 큐를 만들 때의 Top과 Rear 값은 -1이고, Rear는 가장 먼저 들어온 데이터의 위치를 관리해야 하기 때문에
만약 데이터가 원래 비어있는 상태 ( Top = -1 / Rear = -1 일 때 ) 에 데이터가 들어온다면 Rear 값을 0으로 만들어 이후 데이터 삭제에 대비한다.
큐 - Dequeue
큐에서 데이터를 꺼내는 것을 Dequeue 라고 한다. 마찬가지로 단순 데이터를 꺼내는 행위이기 때문에 O(1)의 시간복잡도를 가진다.

현재 가장 먼저 들어온 데이터는 0번째 ( Rear : 0 ) 이기 때문에, 0번째 데이터를 삭제한다. Pop과 마찬가지로 꺼낸 데이터를 반환한다.
Dequeue를 코드로 구현하면 다음과 같다.
int queue[SIZE];
int top = -1;
int rear = -1;
int dequeue() {
return queue[rear++];
}
큐 - Empty, Full
??? : 어? enqueue와 dequeue 과정에서 큐에 데이터가 없거나 가득 찼을 때도 고려해야 하는 거 아닌가요?
이 의문점이 든다면 구조에 대한 이해가 한 층 더 올라갔음을 자만해도 된다.
그렇다, 단순 enqueue 과정과 dequeue 과정만 구현하고 오버플로우 및 언더플로우를 고려하지 않았다!
큐에서도 데이터가 비어있을 때 참을 반환하는 Empty, 데이터가 가득 차있을 때 참을 반환하는 Full을 사용한다.
int queue[SIZE];
int top = -1;
int rear = -1;
int empty() {
if ((top == -1 && rear == -1) || rear > top) return 1;
else return 0;
}
int full() {
if (top == /** 큐 최대 사이즈 **/) return 1;
else return 0;
}full 은 동일하나, top이 -1이고 rear가 -1일 때 혹은 rear 가 top 보다 클 때를 큐가 비어있음으로 가정한다.
top이 -1이고 rear가 -1일 때는 데이터가 비어있는 초기 상태를 말하지만 그 다음 조건은 이해가 되지 않을 수 있다.

데이터를 계속 삭제하여 큐를 비우면, Rear는 계속 증가되면서 Top보다 커지게 된다. 이 때문에 Rear가 Top보다 클 때 큐가 비어있다는 조건을 추가해야 한다.
이를 이용해 enqueue와 dequeue 함수를 다음과 같이 수정할 수 있다.
void enqueue(int x) {
if(!full()) {
if (rear == -1)
rear = 0;
queue[++top] = x;
}
else printf("Queue is Full!");
}
int dequeue() {
if(!empty()) return queue[rear++];
else printf("Queue is Empty!");
}
큐 - 구조 재사용
이정도면 큐의 원리를 배웠지만, 큐를 계속 사용하다보면 문제점이 발생한다.
방금 큐에 들어있던 데이터를 모두 삭제했을 때의 과정을 이어서 살펴보자.

큐에서 데이터를 모두 지운 후 데이터를 다시 추가했을 때, 정상적으로 데이터가 추가되긴 한다. ( Rear 가 가장 낮은 위치에 저장된 7을 가리키고 있고, Top도 가장 높은 위치에 저장된 7을 잘 가리킴 )
그러나, 이런 방식으로 지속적으로 사용하면 빨간색 영역은 앞으로 전혀 사용하지 않게 된다.
기존에 스택에서는 스택을 끝까지 비울 때 Top이 다시 -1로 돌아가니 깔끔하게 사용할 수 있었지만, 지금의 방식은 데이터 추가가 계속해서 Top에서 이루어지고 있으므로 기존에 사용하던 영역은 다시 사용할 수 없다.
이 때, dequeue 과정에서 만약 데이터가 전부 비워졌다면 Top 과 Rear 를 처음 상태 (-1) 로 돌려준다면 맨 처음 상태로 돌아간 것처럼 사용할 수 있다!
int dequeue() {
if(!empty()) {
int value = queue[rear++];
if (rear > top) {
rear = -1;
top = -1;
}
return value;
}
}
다음과 같이 큐 구조를 재사용하는 것이 가능해진다.
큐 - 원형 큐

우리가 배운 큐 자료 구조를 원형적으로 사용하는 것 또한 가능하다. 방금 언급했던 큐의 일부 부분을 사용하지 못할 때의 문제점을 해결하는 다른 방법이다.
void enqueue(int x) {
if(!full()) {
if (rear == -1)
rear = 0;
top = (top + 1) % SIZE; // 99, 100, 0, 1 ...
queue[top] = x;
}
}
int dequeue() {
if(!empty()) {
int value = queue[rear];
rear = (rear + 1) % SIZE; // 99, 100, 0, 1 ...
return value;
}
}모듈러 연산 ( 나머지 연산 ) 을 이용해 top과 rear 값을 단순 증가시키는 것이 아닌 순환하도록 증가시키면 큐를 원형적으로 사용하는 것이 가능하다. 여기서는 간단히 소개하고 넘어간다.
정리
큐에서 한 쪽 끝에서 데이터를 추가하는 것을 Enqueue, 다른 한 쪽 끝에서 데이터를 꺼내는 것을 Dequeue 라고 한다.
큐에 데이터가 가득 차면 Full, 스택이 비었다면 Empty 상태이다.
앞에서 예시로 들었던 버스 문제를 큐로 풀이해보자.

for (int i = 0; i < n; i++) {
char word[100];
scanf("%s", word);
if('0' <= word[0] && word[0] <= '9') { // 들어온 첫 번째 단어가 숫자일 때
char tmpin[100]; // In 입력받기
scanf("%s", tmpin);
int x = atoi(word);
enqueue(x); // 숫자로 변환 후 Enqueue
}
else { // 들어온 첫 번째 단어가 Out
int tmp = dequeue();
}
}
for (int i = rear; i < top; i++) { // Rear ~ Top 까지 큐의 데이터 출력
printf("%d ", queue[i]);
}승차한 사람의 번호는 enqueue를 이용하고, 하차 시 dequeue 를 이용하여 큐 자료 구조로 관리해주면 편하게 버스에 남은 사람들을 승차한 순서대로 구할 수 있다.
큐 구현 코드
// C : Queue implementation
#define SIZE 100
int queue[SIZE];
int top = -1;
int rear = -1;
int empty() {
if ((top == -1 && rear == -1) || rear > top) return 1;
else return 0;
}
int full() {
if (top == SIZE - 1) return 1;
else return 0;
}
void enqueue(int x) {
if(!full()) {
if (rear == -1)
rear = 0;
queue[++top] = x;
}
}
int dequeue() {
if(!empty()) {
int value = queue[rear++];
if (rear > top) {
rear = -1;
top = -1;
}
return value;
}
}
큐 - 연습 문제
1. 큐
https://www.acmicpc.net/problem/10845
10845번: 큐
첫째 줄에 주어지는 명령의 수 N (1 ≤ N ≤ 10,000)이 주어진다. 둘째 줄부터 N개의 줄에는 명령이 하나씩 주어진다. 주어지는 정수는 1보다 크거나 같고, 100,000보다 작거나 같다. 문제에 나와있지
www.acmicpc.net

기본적인 큐를 적용할 수 있는 문제.
2. 큐 2
https://www.acmicpc.net/problem/18258
18258번: 큐 2
첫째 줄에 주어지는 명령의 수 N (1 ≤ N ≤ 2,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 명령이 하나씩 주어진다. 주어지는 정수는 1보다 크거나 같고, 100,000보다 작거나 같다. 문제에 나와있지
www.acmicpc.net

위와 유사한 문제.
3. 카드2
https://www.acmicpc.net/problem/2164
2164번: 카드2
N장의 카드가 있다. 각각의 카드는 차례로 1부터 N까지의 번호가 붙어 있으며, 1번 카드가 제일 위에, N번 카드가 제일 아래인 상태로 순서대로 카드가 놓여 있다. 이제 다음과 같은 동작을 카드가
www.acmicpc.net

큐 원리를 이용한 연습 문제.
'-- 예전 기록 > Algorithm Tutorial' 카테고리의 다른 글
| [ Algorithm ] 재귀 (2) | 2023.06.30 |
|---|---|
| [ Algorithm ] 깊이 우선 탐색과 너비 우선 탐색 (4) | 2023.06.28 |
| [ Algorithm ] 느리게 갱신되는 세그먼트 트리 (0) | 2023.06.18 |
| [ Algorithm ] 세그먼트 트리 (0) | 2023.05.26 |
| [ Algorithm ] 스택 (0) | 2023.04.04 |