
도입
이 글은 그래프 탐색에서 사용할 수 있는 깊이 우선 탐색 (DFS, Depth-First Search) 과 너비 우선 탐색 (BFS, Breadth-First Search) 에 대한 개념 설명을 담고 있습니다. 개인적으로 자료 구조 분야에서 스택 및 큐 개념을 배운 이후 중간 단계를 건너뛰고 바로 DFS와 BFS를 배우면서 PS에 입문한 사람으로써, DFS와 BFS는 실버 시절 제가 많은 실버 문제와 골드 문제를 풀 수 있도록 도와준 알고리즘입니다. 그래프 탐색이라고 해서 단순 그래프 측면이 아닌 다양한 방식으로 응용이 가능한 알고리즘이기에, 익힌다면 여러 분야에서 실전적으로 활용할 수 있을 것입니다. DFS와 BFS의 기본적인 개념을 응용 방식과 함께 배우고 풀이하는 것이 이 글의 목적입니다.
본 글은 C를 기반으로 작성되었습니다.
다음 알고리즘에 대한 이해가 필요합니다!
재귀 (Recursion) : https://readytojoin.tistory.com/83
스택 (Stack) : https://readytojoin.tistory.com/35
큐 (Queue) : https://readytojoin.tistory.com/77
그래프 이론 (Graph Theory)
접근
https://www.acmicpc.net/problem/2606
2606번: 바이러스
첫째 줄에는 컴퓨터의 수가 주어진다. 컴퓨터의 수는 100 이하인 양의 정수이고 각 컴퓨터에는 1번 부터 차례대로 번호가 매겨진다. 둘째 줄에는 네트워크 상에서 직접 연결되어 있는 컴퓨터 쌍
www.acmicpc.net
다음과 같은 문제를 예시로 들어보자.
이것도 구현해보시지
실버 상위 문제부터 연결된 영역을 탐색해야 한다던가, 목적지로 가는 최소 경로를 계산해야 한다던가... 등등 탐색을 요하는 문제가 등장하기 시작한다. 예시 문제도 1번 컴퓨터와 연결된 컴퓨터의 개수를 파악해야 하는 문제이다.
사실 입력 범위가 크지 않기 때문에 직접 구현을 해도 되지만... 따져야 할 것들이 너무 많다!

물론 구현해도 된다. 하지만 필자는 편한 방법이 있으면 그걸 쓰자는 주의이기 때문에 그래프 상에서 연결된 부분을 탐색할 수 있는 깊이 우선 탐색 & 너비 우선 탐색 알고리즘을 사용하고자 한다.
깊이 우선 탐색 ( DFS, Depth-First Search )
깊이 우선 탐색은 그래프를 탐색할 때 최대한 깊이 들어가며 탐색하는 알고리즘이다. 현재 탐색하는 노드부터 더 이상 탐색할 수 있는 노드가 없을 때까지 깊게 끝까지 탐색한 후 돌아오며, 스택 구조나 재귀를 이용해 구현할 수 있다.
정점의 개수가 $N$, 간선의 개수가 $E$일 때 시간 복잡도는 다음과 같다.
인접 행렬 : $O(N^2)$
인접 리스트 : $O(N + E)$
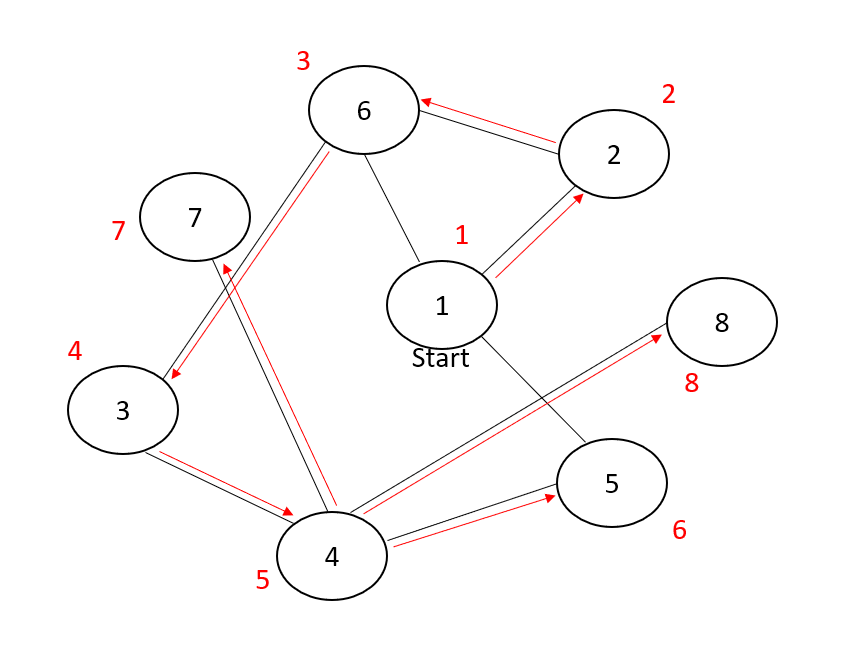
DFS ( 스택 ) - 동작 과정
DFS 를 스택으로 구현했을 때 동작 과정을 천천히 살펴보자. 탐색은 낮은 번호 순서대로 진행한다고 가정한다.
동작 과정에 필요한 구조는 다음과 같다.
1. 스택 : 방문한 노드들의 정보를 저장한다.
2. Visited 배열 : 이 노드를 방문했는지에 대한 여부를 저장한다. ( 1 : 방문함 / 0 : 방문하지 않음 )
먼저, 시작점 노드를 스택에 저장한다.
1번 노드에 도달했으므로, Visited[1] 를 1로 설정한다.

1번 노드에 연결된 노드들 ( 6번, 2번, 5번 ) 중 낮은 번호를 가진 노드는 2번 노드기에 2번 노드를 탐색한다.
2번 노드에 도착한다면, 스택에 2번 노드를 저장한다.
2번 노드에 도달했으므로, Visited[2] 를 1로 설정한다.

2번 노드에 연결된 노드들 ( 6번, 1번 ) 중 낮은 번호를 가진 노드는 1번 노드이지만, 1번 노드의 방문 여부는 이미 1로 설정되었다. ( Visited[1] = 1 )
따라서, 방문하지 않은 노드들 중 낮은 번호를 가진 노드는 6번 노드기에 6번 노드를 탐색한다.
6번 노드에 도착했다면, 스택에 6번 노드를 저장한다.
6번 노드에 도달했으므로, Visited[6] 를 1로 설정한다.
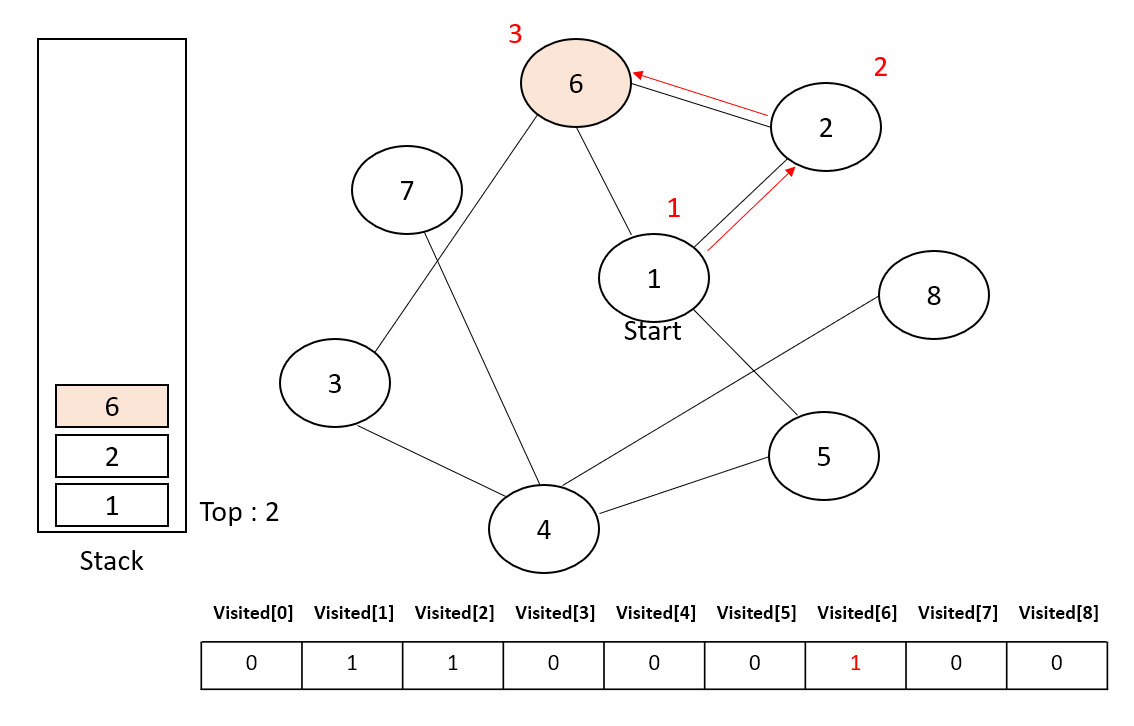
6번 노드에 연결된 노드들 ( 3번, 1번, 2번 ) 중 방문하지 않았으며 낮은 번호를 가진 노드는 3번 노드기에 3번 노드를 탐색하고, 3번 노드에 도착했다면 스택에 3번 노드를 저장한 뒤 Visited[3] 를 1로 설정한다.

3번 노드에 연결된 노드들 ( 4번, 6번 ) 중 방문하지 않았으며 낮은 번호를 가진 노드는 4번 노드기에 4번 노드를 탐색하고, 4번 노드에 도착했다면 스택에 4번 노드를 저장한 뒤 Visited[4] 를 1로 설정한다.

4번 노드에 연결된 노드들 ( 3번, 7번, 8번, 5번 ) 중 방문하지 않았으며 낮은 번호를 가진 노드는 5번 노드기에 5번 노드를 탐색하고, 5번 노드에 도착했다면 스택에 5번 노드를 저장한 뒤 Visited[5] 를 1로 설정한다.

5번 노드에 연결된 노드들 ( 1번, 4번 ) 중 방문하지 않은 노드가 없다! 더 이상 탐색할 노드가 없는 5번 노드까지 깊숙히 탐색했으므로, 5번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다.
이때 돌아갈 순서는 스택에 저장되어 있다!

스택의 Top 에 있는 요소는 현재 탐색하고 있는 노드를 나타내고, ( 지금 도달했을 때 스택에 저장했으니 ) 이 Top 에 있는 요소를 Pop 하면 이전에 다 탐색하지 못하고 스택에 저장했던 노드로 돌아갈 수 있다.
따라서, 5번 노드를 Pop 하고 4번 노드로 되돌아 왔다.
4번 노드에 연결된 노드들 ( 3번, 7번, 8번, 5번 ) 중 방문하지 않았으며 낮은 번호를 가진 노드는 7번 노드기에 7번 노드를 탐색하고, 7번 노드에 도착했다면 스택에 7번 노드를 저장한 뒤 Visited[7] 를 1로 설정한다.

7번 노드에 연결된 노드는 4번 노드뿐이므로 더 이상 탐색할 노드가 없다. 7번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다. 스택의 Top 에 있는 7번 노드를 Pop 하여 이전 노드로 돌아간다.

4번 노드에 연결된 노드들 ( 3번, 7번, 8번, 5번 ) 중 방문하지 않았으며 낮은 번호를 가진 노드는 8번 노드기에 8번 노드를 탐색하고, 8번 노드에 도착했다면 스택에 8번 노드를 저장한 뒤 Visited[8] 를 1로 설정한다.
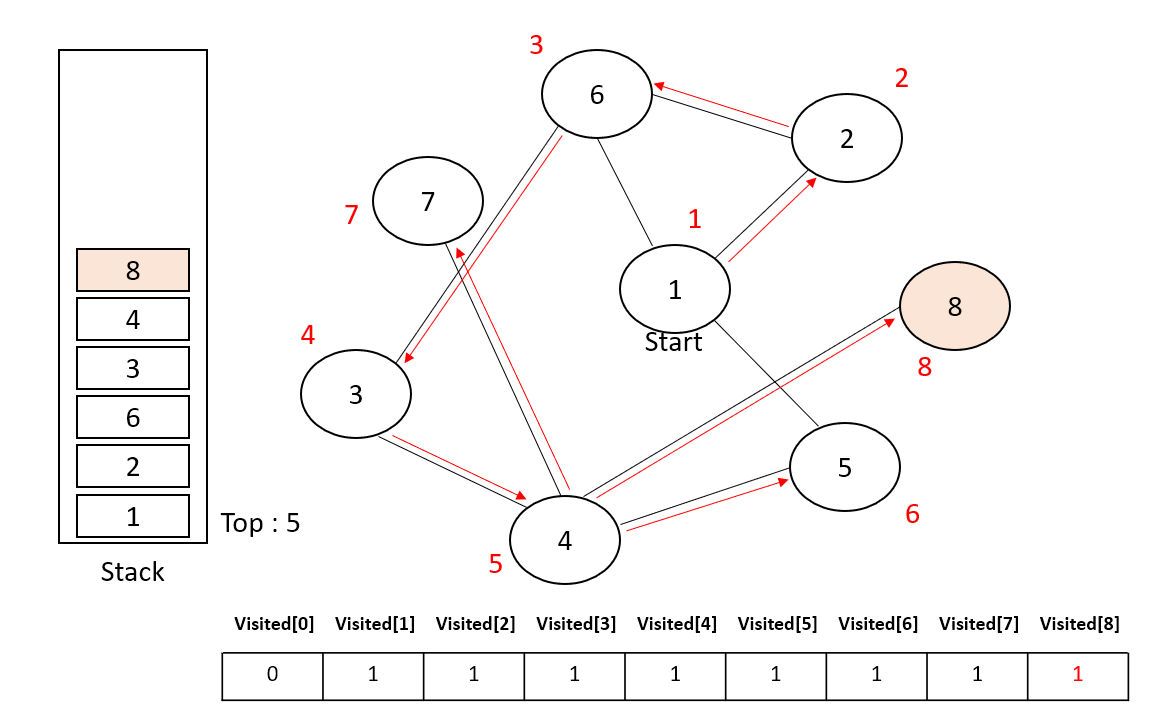
8번 노드에 연결된 노드는 5번 노드뿐이므로 더 이상 탐색할 노드가 없다. 8번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다. 스택의 Top 에 있는 8번 노드를 Pop 하여 이전 노드로 돌아간다.

4번 노드에 연결된 노드들 중 더 이상 탐색할 노드가 없다. 4번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다. 스택의 Top 에 있는 4번 노드를 Pop 하여 이전 노드로 돌아간다.

3번 노드에 연결된 노드들 중 더 이상 탐색할 노드가 없다. 3번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다. 스택의 Top 에 있는 3번 노드를 Pop 하여 이전 노드로 돌아간다.

6번 노드에 연결된 노드들 중 더 이상 탐색할 노드가 없다. 6번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다. 스택의 Top 에 있는 6번 노드를 Pop 하여 이전 노드로 돌아간다.

2번 노드에 연결된 노드들 중 더 이상 탐색할 노드가 없다. 2번 노드는 완전히 탐색했고 다시 이전 노드로 돌아갈 차례이다. 스택의 Top 에 있는 2번 노드를 Pop 하여 이전 노드로 돌아간다.

1번 노드에 연결된 노드들 중 더 이상 탐색할 노드가 없다. 스택의 Top 에 있는 1번 노드를 Pop 한다.

스택이 전부 비워졌다! 스택을 이용해 깊이순으로 그래프를 탐색하는 것이 가능하다.
이 과정을 코드로 구현하면 다음과 같다.
void dfs(int start) {
push(start); // 시작점 Push
visited[start] = 1; // 시작점 방문 체크
printf("Search %d\n", start); // DEBUG
while (!empty()) { // 스택이 비어있지 않다면 반복
int now = topNode(); // 지금 Top 에 있는 노드
int searching = 0; // 현재 탐색중인 노드에서 더 탐색할 노드가 있는가?
for(int i = 1; i < MAX; i++) { // 1번 노드부터 MAX - 1번 노드까지
if (edge[now][i] == 1 && visited[i] == 0) {
// now -> i 로 가는 간선이 있는지, 그리고 방문하지 않았는지
push(i); // i번 노드 Push
visited[i] = 1; // i번 노드 방문 체크
printf("Search %d\n", i); // DEBUG
searching = 1; // 더 탐색할 노드가 있음
break;
}
}
if (searching == 0) pop(); // 더 탐색할 노드가 없을 시 돌아가기
}
}탐색할 노드를 찾아 스택에 Push 한다면, 다음 반복 시 Push 한 노드가 now로 할당되어 그래프를 깊숙히 탐색할 수 있다.
1번 노드부터 MAX - 1번 노드까지 찾다가 더 이상 탐색할 노드가 없을 시 searching 변수가 0으로 변동되지 않아 pop() 을 진행하여 이전 노드로 되돌아간다.
Search 1
Search 2
Search 6
Search 3
Search 4
Search 5
Search 7
Search 8
- 전체 코드
#include <stdio.h>
#define MAX 101
int edge[MAX][MAX] = {0,};
int stack[MAX];
int top = -1;
int visited[MAX] = {0,};
int empty() {
if (top == -1) return 1;
else return 0;
}
int full() {
if (top == MAX - 1) return 1;
else return 0;
}
void push(int x) {
if (!full()) stack[++top] = x;
}
void pop() {
if (!empty()) top -= 1;
}
int topNode() {
if (!empty()) return stack[top];
}
void addEdge(int start, int end) {
edge[start][end] = 1;
}
void dfs(int start) {
push(start); // 시작점 Push
visited[start] = 1; // 시작점 방문 체크
printf("Search %d\n", start); // DEBUG
while (!empty()) { // 스택이 비어있지 않다면 반복
int now = topNode(); // 지금 Top 에 있는 노드
int searching = 0; // 현재 탐색중인 노드에서 더 탐색할 노드가 있는가?
for(int i = 0; i < MAX; i++) {
if (edge[now][i] == 1 && visited[i] == 0) {
// now -> i 로 가는 간선이 있는지 AND 방문하지 않았는지
push(i); // i번 노드 Push
visited[i] = 1; // i번 노드 방문 체크
printf("Search %d\n", i); // DEBUG
searching = 1; // 더 탐색할 노드가 있음
break;
}
}
if (searching == 0) pop(); // 더 탐색할 노드가 없을 시 돌아가기
}
}
int main(void) {
// Setting
addEdge(1, 2); addEdge(1, 5); addEdge(1, 6);
addEdge(2, 1); addEdge(2, 6);
addEdge(3, 4); addEdge(3, 6);
addEdge(4, 3); addEdge(4, 5); addEdge(4, 7); addEdge(4, 8);
addEdge(5, 1); addEdge(5, 4);
addEdge(6, 2); addEdge(6, 3);
addEdge(7, 4);
addEdge(8, 4);
dfs(1);
return 0;
}
DFS ( 재귀 ) - 동작 과정
DFS를 스택이 아닌 재귀로 구현할 수 있다.
재귀 알고리즘 특성 상, 간단한 코드로 작성할 수 있기에 스택으로 구현한 것보다 코드가 단순하다.
void dfs(int now) {
visited[now] = 1; // 현재 노드 방문 처리
printf("Search %d\n", now);
for (int i = 1; i < MAX; i++) { // 1번 노드부터 MAX - 1번 노드까지
if (edge[now][i] == 1 && visited[i] == 0) {
// now -> i 로 가는 간선이 있는지 AND 방문하지 않았는지
dfs(i); // i번 노드 탐색
}
}
}Search 1
Search 2
Search 6
Search 3
Search 4
Search 5
Search 7
Search 8

너비 우선 탐색 ( BFS, Breadth-First Search )
너비 우선 탐색은 그래프를 탐색할 때 가까운 노드부터 퍼져가며 탐색하는 알고리즘이다. 현재 탐색하는 노드에 연결된 노드들을 전부 탐색한 후, 그 노드들에 연결된 노드들을 전부 탐색하고.... 마치 시작 노드부터 퍼져나가는 것처럼 탐색한다. 큐를 이용해 구현할 수 있다.
정점의 개수가 $N$, 간선의 개수가 $E$일 때 시간 복잡도는 다음과 같다.
인접 행렬 : $O(N^2)$
인접 리스트 : $O(N + E)$

BFS ( 큐 ) - 동작 과정
BFS 를 큐로 구현했을 때 동작 과정을 천천히 살펴보자. 탐색은 낮은 번호 순서대로 진행한다고 가정한다.
먼저, 시작점 노드를 큐에 저장한다. 시작점 노드를 방문 처리하는 것도 잊지 말자.

현재 탐색 중인 1번 노드와 연결된 노드들을 탐색하자.
탐색하면서 방문한 노드는 큐에 넣고, 방문 처리를 진행한다.



1번 노드와 연결된 노드들을 전부 탐색했다.
큐에 남아있는 1번 노드는 Dequeue 하여 삭제하고, 큐에 남은 나머지 노드들을 차례대로 탐색한다. ( Front 부터 진행 )

연결된 노드가 없을 시 Dequeue 하여 삭제하고, 큐에 남은 다음 노드를 탐색한다.

DFS와 마찬가지로, Visited 배열을 이용해 이미 방문한 노드는 방문하지 않는다.







큐가 전부 비워졌다! 큐를 이용해 너비를 우선하여 그래프를 탐색하는 것이 가능하다.
이 과정을 코드로 구현하면 다음과 같다.
void bfs(int start) {
enqueue(start); // 시작점 Enqueue
visited[start] = 1; // 시작점 방문 체크
printf("Search %d\n", start); // DEBUG
while(!empty()) { // 큐가 비어있지 않다면 반복
int now = rearNode(); // 지금 Rear (Front) 에 있는 노드
for (int i = 1; i < MAX; i++) { // 1번 노드부터 MAX - 1번 노드까지
if (edge[now][i] == 1 && visited[i] == 0) {
// now -> i 로 가는 간선이 있는지, 그리고 방문하지 않았는지
enqueue(i); // i번 노드 Enqueue
visited[i] = 1; // i번 노드 방문 체크
printf("Search %d\n", i); // DEBUG
}
}
dequeue(); // 현재 노드 탐색 완료. Enqueue
}
}Search 1
Search 2
Search 5
Search 6
Search 4
Search 3
Search 7
Search 8
- 전체 코드
#include <stdio.h>
#define MAX 101
int edge[MAX][MAX] = {0,};
int queue[MAX];
int top = -1;
int rear = -1;
int visited[MAX] = {0,};
int empty() {
if (top == -1 && rear == -1) return 1;
else return 0;
}
int full() {
if (top == MAX - 1) return 1;
else return 0;
}
void enqueue(int x) {
if(!full()) {
if (top == -1) rear = 0;
queue[++top] = x;
}
}
void dequeue() {
if(!empty()) {
rear += 1;
if (rear > top) {
top = -1;
rear = -1;
}
}
}
int rearNode() {
return queue[rear];
}
void addEdge(int start, int end) {
edge[start][end] = 1;
}
void bfs(int start) {
enqueue(start); // 시작점 Enqueue
visited[start] = 1; // 시작점 방문 체크
printf("Search %d\n", start); // DEBUG
while(!empty()) { // 큐가 비어있지 않다면 반복
int now = rearNode(); // 지금 Rear (Front) 에 있는 노드
for (int i = 1; i < MAX; i++) { // 1번 노드부터 MAX - 1번 노드까지
if (edge[now][i] == 1 && visited[i] == 0) {
// now -> i 로 가는 간선이 있는지, 그리고 방문하지 않았는지
enqueue(i); // i번 노드 Enqueue
visited[i] = 1; // i번 노드 방문 체크
printf("Search %d\n", i); // DEBUG
}
}
dequeue(); // 현재 노드 탐색 완료. Enqueue
}
}
int main(void) {
// Setting
addEdge(1, 2); addEdge(1, 5); addEdge(1, 6);
addEdge(2, 1); addEdge(2, 6);
addEdge(3, 4); addEdge(3, 6);
addEdge(4, 3); addEdge(4, 5); addEdge(4, 7); addEdge(4, 8);
addEdge(5, 1); addEdge(5, 4);
addEdge(6, 2); addEdge(6, 3);
addEdge(7, 4);
addEdge(8, 4);
bfs(1);
return 0;
}이제 DFS와 BFS를 문제에 적용해보자.
2606 : 바이러스
https://www.acmicpc.net/problem/2606
2606번: 바이러스
첫째 줄에는 컴퓨터의 수가 주어진다. 컴퓨터의 수는 100 이하인 양의 정수이고 각 컴퓨터에는 1번 부터 차례대로 번호가 매겨진다. 둘째 줄에는 네트워크 상에서 직접 연결되어 있는 컴퓨터 쌍
www.acmicpc.net
간선을 입력받아 저장하여 이를 토대로 1번 컴퓨터를 기준으로 한 DFS, BFS를 실행해주면 된다.
- DFS ( 재귀 ) 풀이
#include <stdio.h>
#define MAX 101
int edge[MAX][MAX] = {0,};
int visited[MAX] = {0,};
int dfs(int now) {
int cnt = 1;
visited[now] = 1;
for (int i = 1; i < MAX; i++) {
if (edge[now][i] == 1 && visited[i] == 0)
cnt += dfs(i);
}
return cnt;
}
int main(void) {
int n, m;
scanf("%d", &n);
scanf("%d", &m);
for(int i = 0; i < m; i++) {
int start, end;
scanf("%d %d", &start, &end);
edge[start][end] = 1;
edge[end][start] = 1;
}
int result = dfs(1);
printf("%d", result - 1); // -1 : Start (1)
return 0;
}
- BFS 풀이
#include <stdio.h>
#define MAX 101
int edge[MAX][MAX] = {0,};
int queue[MAX];
int top = -1;
int rear = -1;
int visited[MAX] = {0,};
int empty() {
if (top == -1 && rear == -1) return 1;
else return 0;
}
int full() {
if (top == MAX - 1) return 1;
else return 0;
}
void enqueue(int x) {
if(!full()) {
if (top == -1) rear = 0;
queue[++top] = x;
}
}
void dequeue() {
if(!empty()) {
rear += 1;
if (rear > top) {
top = -1;
rear = -1;
}
}
}
int rearNode() {
return queue[rear];
}
int bfs(int start) {
int cnt = 0;
enqueue(start); // 시작점 Enqueue
visited[start] = 1; // 시작점 방문 체크
while(!empty()) { // 큐가 비어있지 않다면 반복
int now = rearNode(); // 지금 Rear (Front) 에 있는 노드
for (int i = 1; i < MAX; i++) { // 1번 노드부터 MAX - 1번 노드까지
if (edge[now][i] == 1 && visited[i] == 0) {
// now -> i 로 가는 간선이 있는지, 그리고 방문하지 않았는지
enqueue(i); // i번 노드 Enqueue
visited[i] = 1; // i번 노드 방문 체크
cnt += 1;
}
}
dequeue(); // 현재 노드 탐색 완료. Enqueue
}
return cnt;
}
int main(void) {
int n, m;
scanf("%d", &n);
scanf("%d", &m);
for(int i = 0; i < m; i++) {
int start, end;
scanf("%d %d", &start, &end);
edge[start][end] = 1;
edge[end][start] = 1;
}
int result = bfs(1);
printf("%d", result);
return 0;
}
'-- 예전 기록 > Algorithm Tutorial' 카테고리의 다른 글
| [ Algorithm ] 백트래킹 (1) | 2023.11.13 |
|---|---|
| [ Algorithm ] 재귀 (2) | 2023.06.30 |
| [ Algorithm ] 큐 (0) | 2023.06.25 |
| [ Algorithm ] 느리게 갱신되는 세그먼트 트리 (0) | 2023.06.18 |
| [ Algorithm ] 세그먼트 트리 (0) | 2023.05.26 |