
문제
각각 N(1 ≤ N ≤ 2,000)개의 쌍으로 이루어진 2N개의 정점과 M(1 ≤ M ≤ N×(N-1)/2)개의 간선으로 구성된 이분그래프가 주어질 때 서로 교차하는 총 개수를 구하는 것이다.
- 교차 조건 : 한 독립 집합 A와 다른 독립 집합 B가 연결된 두 개의 간선을 (A1, B1), (A2, B2)라 한다면 A1 < A2, B1 > B2 또는 A1 > A2, B1 < B2를 만족한다면 두 간선을 교차한다고 한다.
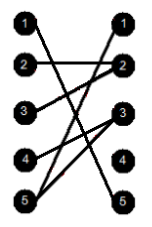
예를 들어 위에 예에서 (3, 2)는 (1, 5)와 (5, 1)과 교차한다. 이 문제를 해결하는 프로그램을 작성하시오.
입력
첫 줄에 N과 간선의 개수 M이 주어진다. 그 다음 줄부터 M+1번째 줄까지 두 개의 수(i, j)가 주어지는데 이는 왼쪽 그룹의 i번 정점과 오른쪽 그룹의 j번 정점을 연결하는 간선이 있다는 의미이다. 중복되는 간선이 입력으로 주어지지 않는다.
출력
입력에서 주어진 간선이 교차하는 총 개수를 출력한다.
풀이 과정
세그먼트 트리로 교차 선의 개수를 셀 수 있다. (i, j) 간선들을 오름차순으로 정렬하고, 순서대로 간선을 배치하면서 (트리 노드 j 번째 에 1 증가), [j+1, n] 사이 구간 합이 교차한 개수 선이다.
#include <stdio.h>
#define QSIZE 2000000
#define NSIZE 2000
typedef long long LL;
int query[QSIZE][2];
int query_size = 0;
int sort_query[QSIZE][2];
LL tree[NSIZE * 4] = { 0, };
void query_merge(int start, int mid, int end) {
int leftidx = start;
int rightidx = mid + 1;
int allidx = start;
while (leftidx <= mid && rightidx <= end) {
if (query[leftidx][0] < query[rightidx][0]) {
sort_query[allidx][0] = query[leftidx][0];
sort_query[allidx][1] = query[leftidx][1];
allidx += 1;
leftidx += 1;
}
else if (query[leftidx][0] > query[rightidx][0]) {
sort_query[allidx][0] = query[rightidx][0];
sort_query[allidx][1] = query[rightidx][1];
allidx += 1;
rightidx += 1;
}
else {
if (query[leftidx][1] < query[rightidx][1]) {
sort_query[allidx][0] = query[leftidx][0];
sort_query[allidx][1] = query[leftidx][1];
allidx += 1;
leftidx += 1;
}
else {
sort_query[allidx][0] = query[rightidx][0];
sort_query[allidx][1] = query[rightidx][1];
allidx += 1;
rightidx += 1;
}
}
}
while (leftidx <= mid) {
sort_query[allidx][0] = query[leftidx][0];
sort_query[allidx][1] = query[leftidx][1];
allidx += 1;
leftidx += 1;
}
while (rightidx <= end) {
sort_query[allidx][0] = query[rightidx][0];
sort_query[allidx][1] = query[rightidx][1];
allidx += 1;
rightidx += 1;
}
for (int i = start; i <= end; i++) {
query[i][0] = sort_query[i][0];
query[i][1] = sort_query[i][1];
}
}
void query_merge_sort(int start, int end) {
if (start < end) {
int mid = (start + end) / 2;
query_merge_sort(start, mid);
query_merge_sort(mid + 1, end);
query_merge(start, mid, end);
}
}
void update(int start, int end, int idx, int what) {
if (what < start || end < what) return;
if (start == end) {
tree[idx] += 1;
return;
}
int mid = (start + end) / 2;
update(start, mid, idx * 2, what);
update(mid + 1, end, idx * 2 + 1, what);
tree[idx] = tree[idx * 2] + tree[idx * 2 + 1];
}
LL interval_sum(int start, int end, int idx, int left, int right) {
if (end < left || right < start) return 0;
if (left <= start && end <= right) return tree[idx];
int mid = (start + end) / 2;
return interval_sum(start, mid, idx * 2, left, right) + interval_sum(mid + 1, end, idx * 2 + 1, left, right);
}
int main(void) {
int n, m;
scanf("%d %d", &n, &m);
for (int i = 0; i < m; i++) {
int a, b;
scanf("%d %d", &a, &b);
query[query_size][0] = a - 1;
query[query_size++][1] = b - 1;
}
query_merge_sort(0, query_size - 1);
LL result = 0;
for (int i = 0; i < query_size; i++) {
result += interval_sum(0, n - 1, 1, query[i][1], n - 1);
update(0, n - 1, 1, query[i][1] - 1);
}
printf("%lld", result);
return 0;
}'-- 예전 기록 > BOJ' 카테고리의 다른 글
| [ BOJ ] 12895 : 화려한 마을 ( PLATINUM 3 ) / C (0) | 2023.04.03 |
|---|---|
| [ BOJ ] 2342 : Dance Dance Revolution ( GOLD 3 ) / Python (0) | 2023.03.31 |
| [ BOJ ] 1321 : 군인 ( PLATINUM 5 ) / C (0) | 2023.03.31 |
| [ BOJ ] 1306 : 달려라 홍준 ( PLATINUM 5 ) / C (0) | 2023.03.29 |
| [ BOJ ] 2143 : 두 배열의 합 ( GOLD 3 ) / Python (0) | 2023.03.28 |