
문제
프로젝트 하느라 바쁜 득수는 밥 먹을 시간이 부족하다. 그래서 주로 찾는 식당 네 개 중 하나에서 하루에 한 번 밥을 먹는다. 귀찮으면 굶을 때도 있다.
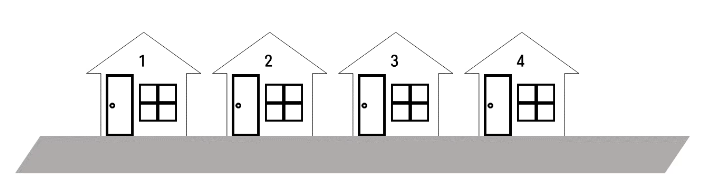
늘 새로운 느낌을 받고 싶었던 득수는 다음과 같은 규칙으로 다음날 갈 식당을 정한다.
- 첫날에는 굶거나, 임의로 원하는 식당 하나를 골라서 간다.
- 어제 굶지 않았다면, 오늘은 식당을 가지 않아도 된다.
- 어제 식당을 가지 않았다면, 오늘은 식당을 가서 밥을 먹어야 한다.
- 오늘 간 식당은 다음날 가지 않는다.
- 오늘 간 식당과 이웃한 식당은 다음날 가지 않는다.
만약 2번 식당을 오늘 갔다면, 다음날 , , 번 식당은 가지 않는다. 따라서 새로운 느낌을 받으려면 번 식당을 가거나 굶어야 한다.
득수가 일 치 식단표를 만들려고 한다. 위 규칙을 따라 식단표를 만들 때 가능한 경우의 수를 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에는 득수가 만들어야 하는 점심 식단의 총 날짜 이 입력으로 들어온다. (1 ≤ N ≤ 200 000)
출력
일 치 식단표를 만들 때 가능한 경우의 수를 1 000 000 007로 나눈 나머지를 출력한다.
풀이 과정
DP 식을 세워 N일째에 할 수 있는 행동의 경우의 수를 센다.
dp[i][j] : j번째 날에 i번째 식당을 가는 경우의 수 (0번째 식당은 굶는 경우의 수) % 1000000007
이전 날에 행동한 경우에 따라 다음 날의 상태를 구하면 되며, 다음은 유의해야 할 점이다.
- 어제 식당을 가지 않았다면, 오늘은 식당을 가서 밥을 먹어야 한다. -> j번째 날에 1 ~ 4번째 식당을 가는 경우의 수는 j - 1번째 날에 굶은 경우의 수를 더해야 한다.
- 오늘 간 식당은 다음날 가지 않는다. / 오늘 간 식당과 이웃한 식당은 다음날 가지 않는다. -> j 번째 날에 1 ~ 4번째 식당을 가는 경우의 수는 j - 1번째 날에 |오늘 갈 식당 - 어제 간 식당| 이 2 이상인 경우의 수를 더해야 한다.
import sys
input = sys.stdin.readline
# 첫날에는 X, O
# 어제 O -> 다음 날 O X
# 어제 X -> 다음 날 O
# 어제 간 식당과 이웃한 식당은 가지 않는다.
n = int(input().rstrip())
dp = [[0 for _ in range(n)] for _ in range(5)]
MOD = 1000000007
# dp[i][j] : i번째 식당을 j번째 날에 가는 경우의 수 (0번은 굶는 경우의 수)
for j in range(n):
if j == 0:
for i in range(5):
dp[i][j] = 1
else:
for i in range(1, 5):
dp[0][j] = (dp[0][j] + dp[i][j-1]) % MOD
for k in range(5):
if k != 0 and abs(k-i) <= 1: continue
dp[i][j] = (dp[i][j] + dp[k][j-1]) % MOD
result = 0
for i in range(5): result += dp[i][-1]
print(result % MOD)'-- 예전 기록 > BOJ' 카테고리의 다른 글
| [ BOJ ] 9372 : 상근이의 여행 ( SILVER 4 ) / Python (0) | 2024.02.01 |
|---|---|
| [ BOJ ] 23350 : K 물류창고 ( SILVER 2 ) / Python (0) | 2024.02.01 |
| [ BOJ ] 15924 : 욱제는 사과팬이야!! ( GOLD 5 ) / Python (1) | 2024.02.01 |
| [ BOJ ] 20127 : Y-수열 ( GOLD 5 ) / Python (0) | 2024.02.01 |
| [ BOJ ] 5547 : 일루미네이션 ( GOLD 4 ) / Python (0) | 2024.02.01 |