커누스-모리스-프랫 알고리즘 (Knuth–Morris–Pratt algorithm, KMP) 은 문자열 S 에서 문자열 A 를 찾고자 할 때 단순히 모든 경우를 다 비교해보면서 찾는 방식 보다는 접두사와 접미사를 이용해 불필요한 문자열 탐색 횟수를 줄여 문자열을 효율적으로 찾아낼 수 있는 문자열 매칭 알고리즘이다.
하나씩 비교하는 문자열 매칭
문자열 S의 길이를 N, 문자열 A의 길이를 M이라 할 때, 문자열 S 에서 문자열 A를 찾을 때의 시간 복잡도는 O(NM) 이다.
S = input()
A = input()
for i in range(len(S)):
for j in range(len(A)):
if S[i+j] != A[j]: break
if j == len(A) - 1: print(i)# Input
abcabcabc
abc
# Output
0
3
6
문자열을 하나하나 비교해보다가 틀린 부분이 있다면 S의 다음 문자로 넘어가는 원리이다. 위 그림에서도 알 수 있듯이 S의 다음 문자로 넘어간다고 해도 바로 동일한 문자열이 매칭되는 것이 아닌 불필요한 탐색 부분이 존재한다.
직접 눈으로 문자열 매칭을 한다고 직관적으로 생각해보자. 우리 눈은 ABC 에서 DEF를 찾지 못했다면 ABC 의 B로 넘어가서 다시 보는 것이 아닌 ABC를 넘기고 다음 단어를 찾는다. 이 원리를 이용해 불필요한 탐색 부분을 줄일 수 없을까?

다음 예시에선 a 와 d 가 달라 전체 매칭에 실패했다. 전체 매칭에 실패했다고 해서 다음 문자로 넘어가서 하나하나 비교하는 방법 대신에, 불필요한 탐색을 건너뛰기 위해 매칭된 문자열의 앞과 뒤에서 동일하게 나오는 부분이 있는지 확인해본다.

매칭된 부분에서 앞 뒤에 ab 라는 동일한 접두사와 접미사가 있다. 이렇게 동일한 패턴이 있다면, 중간 부분을 탐색할 필요 없이 바로 동일 접미사 부분으로 건너뛰면 된다.

따라서, 문자열을 탐색하는 위치를 더 효율적으로 움직이기 위해, 우리는 매칭된 문자열의 접두사와 접미사의 최대 일치 부분을 찾아야 한다.
KMP - 실패 함수
# KMP table
table = [0 for _ in range(len(A))]
i = 0 # 접두사와 접미사의 최대 일치 부분
for j in range(1, len(A)):
while i > 0 and A[i] != A[j]:
i = table[i-1]
if A[i] == A[j]:
i += 1
table[j] = i
먼저, 접두사와 접미사의 최대 일치 부분이 얼마나 되는지 저장하는 테이블을 만들어야 한다. 이때, 문자열이 몇 개 매칭되었는지에 따라서 접두사와 접미사의 최대 일치 부분을 모두 저장해야 한다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | |
| 2 | AB | |
| 3 | ABA | |
| 4 | ABAC | |
| 5 | ABACA | |
| 6 | ABACAB | |
| 7 | ABACABA | |
| 8 | ABACABAB |
그냥 찾고자 하는 문자열 "전체"에서 접두사와 접미사의 최대 일치 부분을 찾으면 되는거 아닌가요? 라고 생각할 수도 있겠지만, 문자열을 찾다가 보면 일부만 매칭되고 틀린 부분이 존재할 수도 있기 때문에, 그 때 얼마나 매칭되었는지에 따라서 탐색을 얼만큼 건너뛸 수 있는지를 판단할 수 있다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | |
| 3 | ABA | |
| 4 | ABAC | |
| 5 | ABACA | |
| 6 | ABACAB | |
| 7 | ABACABA | |
| 8 | ABACABAB |
코드대로 테이블을 채워나가보자. 먼저 길이 1만 매칭된 경우에는 아무것도 매칭되지 않은 경우와 동일하게 다음 S 문자로 이동하여 탐색한다.
# KMP table
table = [0 for _ in range(len(A))]
i = 0 # 접두사와 접미사의 최대 일치 부분
for j in range(1, len(A)):
코드의 다음 부분을 통해 A[0]과 A[1]은 0이 저장되도록 했다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | |
| 4 | ABAC | |
| 5 | ABACA | |
| 6 | ABACAB | |
| 7 | ABACABA | |
| 8 | ABACABAB |
A[0] 과 A[1] 을 비교해 접두사와 접미사가 일치하는지 확인했다. A[0] (A)와 A[1] (B)는 일치하지 않으므로 최대 일치 부분 (i)는 0이다.
if A[i] == A[j]: # A[0] 과 A[1] 은 일치하지 않으므로 i 는 0
i += 1
table[j] = i
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAC | |
| 5 | ABACA | |
| 6 | ABACAB | |
| 7 | ABACABA | |
| 8 | ABACABAB |
매칭된 문자열 길이가 2일 때 최대 일치 부분이 0에서 증가하지 않았다. 그러므로 매칭된 문자열 길이가 3일 때 접두사는 A[0] 에서, 접미사는 A[2] 에서 최대 일치 부분이 1이 되는지 확인한다. (양쪽 끝 문자인 접두사와 접미사를 확인한다.) A[0] (A)와 A[2] (A)는 일치하므로 최대 일치 부분은 (i)는 1 증가하여 1이다.
if A[i] == A[j]: # A[0] 과 A[2] 는 일치하므로 i 는 1
i += 1
table[j] = i
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAC | 0 |
| 5 | ABACA | |
| 6 | ABACAB | |
| 7 | ABACABA | |
| 8 | ABACABAB |
매칭된 문자열 길이가 3일 때 최대 일치 부분이 1이 되었다. 만약 매칭된 문자열 길이가 4일 때 최대 일치 부분이 2가 되려면 매칭된 문자열이 ABAB 이여서 접두사는 A[1]에서, 접미사는 A[3] 에서 동일한지 확인하면 되지만, (A[0]과 A[2] 는 이미 동일하므로 다음 문자를 확인) 현재 매칭된 문자열은 ABAC이다.
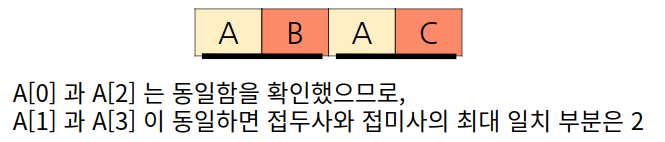
while i > 0 and A[i] != A[j]:
i = table[i-1]
최대 일치 부분이 0보다 크고 접두사와 접미사의 마지막 부분이 동일하지 않다면, 최대 일치 부분(i) 은 매칭된 문자열의 길이가 i-1 일 때의 최대 일치 부분이 된다. 이 부분은 지금은 이해가 되지 않아도 일단 코드를 따라가보자. 이후에 이해할 수 있는 예제가 나온다.
매칭된 문자열의 길이가 i-1 (0) 일 때의 최대 일치 부분은 0이므로 매칭된 문자열 길이가 4일 때의 i 는 0이 된다.
if A[i] == A[j]: # A[0] 과 A[3] 는 일치하지 않으므로 i 는 0
i += 1
table[j] = i
최대 일치 부분 (i) 이 0이 되었기 때문에, 다시 양쪽 끝 문자인 접두사와 접미사의 일치 여부를 확인했지만, A[0] (A) 와 A[3] (C) 는 일치하지 않으므로 최대 일치 부분은 0 이다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAC | 0 |
| 5 | ABACA | 1 |
| 6 | ABACAB | |
| 7 | ABACABA | |
| 8 | ABACABAB |
i 는 0이기에, 양쪽 끝 접두사와 접미사를 확인한다. A[0] (A) 와 A[4] (A)는 일치하므로 최대 일치 부분 (i) 은 1이다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAC | 0 |
| 5 | ABACA | 1 |
| 6 | ABACAB | 2 |
| 7 | ABACABA | |
| 8 | ABACABAB |
매칭된 문자열 길이가 4였을 때 처럼, i가 1이므로 A[1] 과 A[5] 를 비교한다. A[1] (B) 와 A[5] (B) 는 일치하므로 최대 일치 부분 (i) 은 2이다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAC | 0 |
| 5 | ABACA | 1 |
| 6 | ABACAB | 2 |
| 7 | ABACABA | 3 |
| 8 | ABACABAB |
i가 2이므로 A[2] 와 A[6] 을 비교한다. A[2] (A) 와 A[6] (A) 는 일치하므로 최대 일치 부분 (i) 은 3이다.
| 매칭된 문자열 길이 | 매칭된 문자열 | 접두사와 접미사의 최대 일치 부분 (i) |
| 0 | 0 | |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAC | 0 |
| 5 | ABACA | 1 |
| 6 | ABACAB | 2 |
| 7 | ABACABA | 3 |
| 8 | ABACABAB | 2 |
i가 3이므로 A[3]과 A[7] 을 비교한다. A[3] (C) 와 A[7] (B) 는 일치하지 않는다.
while i > 0 and A[i] != A[j]:
i = table[i-1]
다음 코드가 실행되는데, 현재 i 는 3이므로 table[2] 의 값이 i 에 저장된다.
우리는 table[j] = i 를 통해 i 를 저장해왔으므로, A의 2번째 인덱스까지의 접두사와 접미사 최대 일치 부분이 i의 값이 되고, A의 2번째 인덱스까지는 ABA이므로 매칭된 문자열 길이가 3일 때의 접두사와 접미사 최대 일치 부분이다. 따라서 i 는 매칭된 문자열 길이가 3일 때의 접두사와 접미사 최대 일치 부분인 1이 되고, A[1] (B) 와 A[7] (B) 는 동일하므로 반복문이 멈추고 i 는 1 증가하여 2가 된다. 실행 과정을 살펴보자.

우리는 이전에 매칭된 문자열의 길이가 7일 때 최대 일치 부분이 3임을 기록해놓았다. 따라서 i 도 3을 저장하고 있었다.
하지만 다음 접두사와 다음 접미사로 들어가야 했을 A[3] 과 A[7] 이 각각 C와 B로 일치하지 않았다. 우리는 최대 일치 부분이 4가 되지 않음을 알 수 있고, 최대 일치 부분 안에서 또 다른 일치 부분이 있는지 확인해 이를 "이용"해야 한다.
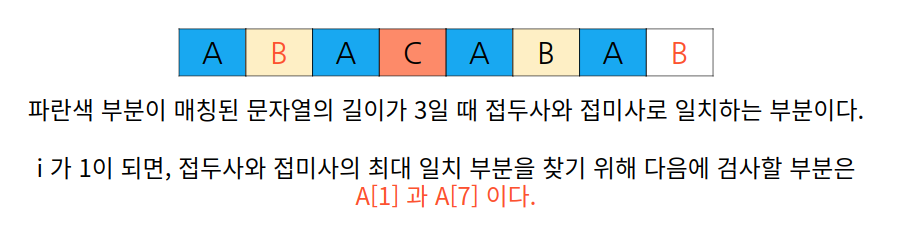
이전에 매칭된 문자열의 길이가 3일 때 최대 일치 부분이 1임을 기록해놓았다. ABA 에서 다음 접두사와 접미사가 공통되지 않으니, 접두사 ABA 와 접미사 ABA는 둘 다 접두사와 접미사로 A 부분을 공통으로 가진다는 사실을 이용해서, 접두사 ABA의 공통 부분 접두사인 A를 접두사로, 접미사 ABA의 공통 부분 접미사인 A를 접미사로 사용한다.
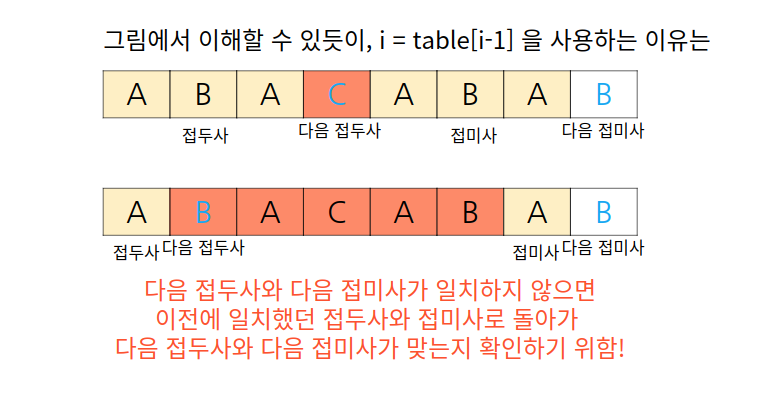
접두사와 접미사가 ABABABA 인 경우라면 ABABA, ABA, A 처럼 이전에 일치했던 공통 부분 접두사와 접미사를 활용해 다음 접두사와 다음 접미사가 맞는지 확인할 수 있도록 하는 역할을 i = table[i-1] 이 한다.
찾으려는 문자열 : ABACABAB
매칭된 길이가 1 : A -> 0
매칭된 길이가 2 : AB -> 0
A[0] A 와 A[1] B는 같지 않음. i 는 0
매칭된 길이가 3 : ABA -> 1
A[0] A 와 A[2] A가 같음. i 는 1
매칭된 길이가 4 : ABAC -> 0
A[1] B와 A[3] C는 같지 않음. i = table[i-1] (0)
A[0] A와 A[3] C는 같지 않음. i 는 0
매칭된 길이가 5 : ABACA -> 1
A[0] A와 A[4] A는 같음. i 는 1
매칭된 길이가 6 : ABACAB -> 2
A[1] B와 A[5] B는 같음. i 는 2
매칭된 길이가 7 : ABACABA -> 3
A[2] A와 A[6] A는 같음. i 는 3
매칭된 길이가 8 : ABACABAB -> 2
A[3] C와 A[7] B는 같지 않음. i = table[i-1] (1)
(매칭된 길이가 7일 때의 접두사와 접미사를, 매칭된 길이가 3일 때의 접두사와 접미사처럼 고려한다.)
ABACABAB
___ ___
A A
_ _
(이후 다시 동일 부분의 끝 문자가 동일한지 확인한다.)
A[1] B와 A[7] B는 같음. i 는 2KMP - 탐색
# KMP
result = []
i = 0
for j in range(len(S)):
while i > 0 and A[i] != S[j]:
i = table[i-1]
if A[i] == S[j]:
i += 1
if i == len(A):
result.append(j - i + 2) # 찾은 문자열의 시작 위치
i = table[i-1]
KMP 실패 함수에서 사용했던 방식처럼, A와 S가 일치할 때 마다 i 를 1씩 증가시키고, 일치하지 않는 부분이 있다면 동일 부분 크기를 감소시키되 끝까지 감소하지 않고 이전 공통 부분 접두사와 접미사까지 감소하여 효율적인 탐색이 가능하도록 한다.
문자열을 완전 매칭했다면 i = table[i-1] 을 한 번 더 진행하여 다음 매칭될 문자열이 있는지 찾는다.
KMP 알고리즘은 이러한 효율적인 탐색 방법으로, 문자열 S에서 문자열 A를 찾고자 할 때 O(N + M) 의 시간 복잡도를 가진다.
출처
커누스-모리스-프랫 알고리즘 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 컴퓨터 과학에서 커누스-모리스-프랫 알고리즘(Knuth–Morris–Pratt algorithm, KMP)은 문자열 중에 특정 패턴을 찾아내는 문자열 검색 알고리즘의 하나이다. 문자열
ko.wikipedia.org
[github.io] 알고리즘 - KMP 알고리즘 : 문자열 검색을 위한 알고리즘
알고리즘 - KMP 알고리즘 : 문자열 검색을 위한 알고리즘
@ 문자열을 검색하려면? : 패턴 매칭
chanhuiseok.github.io
KMP 알고리즘 (문자열 매칭)
모든 kmp 알고리즘 포스팅 중 가장 쉽고 자세하게 kmp 이해해보기 🤗⚙️🦾
velog.io
'알고리즘 문제 풀이 > 알고리즘 설명' 카테고리의 다른 글
| SCC - 강한 연결 요소 찾기 (0) | 2024.08.16 |
|---|---|
| LCA - 최소 공통 조상 찾기 (0) | 2024.08.16 |
| Sparse Table - 희소 배열 (0) | 2024.08.15 |