
문제
Wacław Sierpiński는 폴란드 수학자이다. 어느 날 그는 아래와 같은 방법으로 삼각형을 그리기로 했다.
- 정삼각형 T를 그린다.
- 삼각형 변의 중점을 서로 연결한다. 새롭게 생긴 정삼각형을 T1, T2, T3, T4라고 한다. 아래 그림 중 왼쪽 그림이 해당한다.
- 위의 단계를 삼각형 T1, T2, T3에 대해서 반복한다. 새로운 삼각형은 T11, T12, T13, T14, T21, T22, T23, T24, T31, T32, T33, T34가 된다.
- 1, 2, 3으로 끝나는 모든 삼각형에 대해서 이 방법을 반복한다. 이렇게 생긴 프랙탈을 Sierpinski 삼각형이라고 한다.
삼각형 B가 삼각형 A를 포함하지 않고, A의 한 변 전체가 B의 한 변의 일부일 때, A는 B에 기대고 있다고 한다. 예를 들어, 삼각형 T23은 T24와 T4에 기대고 있지만, T2와 T32에는 기대고 있지 않다. (A가 B에 기대고 있다는 말은 B가 A에 기대고 있다는 말을 포함하지 않는다)
Sierpinski 삼각형의 일부 삼각형 A가 주어진다. 이때, A가 기대고 있는 모든 삼각형 B를 찾는 프로그램을 작성하시오.
입력
첫째 줄에 삼각형 A가 주어진다. 삼각형 A의 이름은 2글자보다 크거나 같고, 50글자보다 작거나 같다.
출력
삼각형 A가 기대고 있는 모든 삼각형을 한 줄에 하나씩 출력한다. 출력하는 순서는 아무 순서나 상관없다.
풀이 과정
기대고 있는 삼각형을 출력하는 순서는 아무 순서나 상관없으므로, 맨 뒷 번호부터 시작한다.
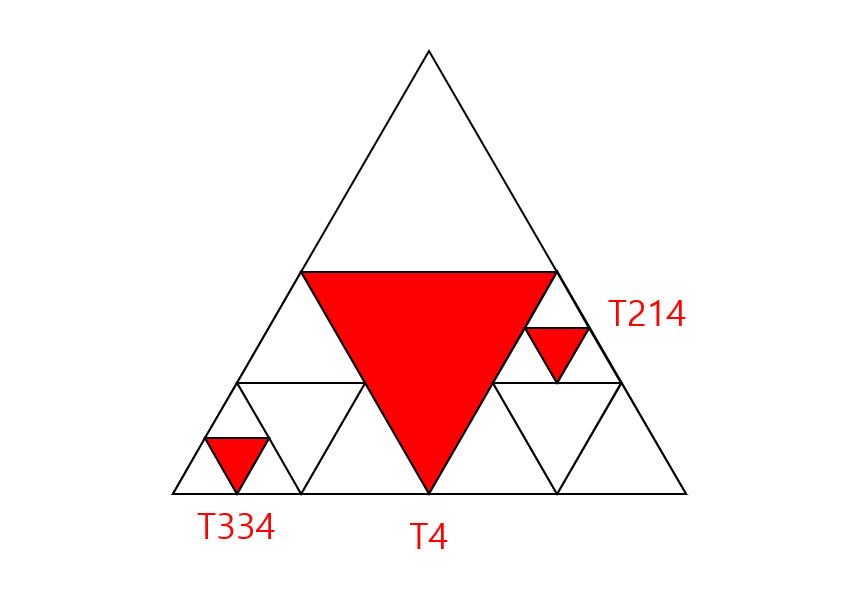
기존에 분할된 부분들을 x라고 할 때, 어느 부분의 Tx4 삼각형이 기대고 있는 삼각형은 Tx1, Tx2, Tx3 이다.
예를 들면, T4 삼각형이 기대고 있는 삼각형은 T1, T2, T3이고,
T214 삼각형이 기대고 있는 삼각형은 T211, T212, T213이고,
T334 삼각형이 기대고 있는 삼각형은 T331, T332, T333 이다.
T4 삼각형은 더 이상 안쪽에서 분할되지 않으므로, 입력된 삼각형의 마지막 부분이 4라면, 3개의 삼각형만 출력하면 된다.
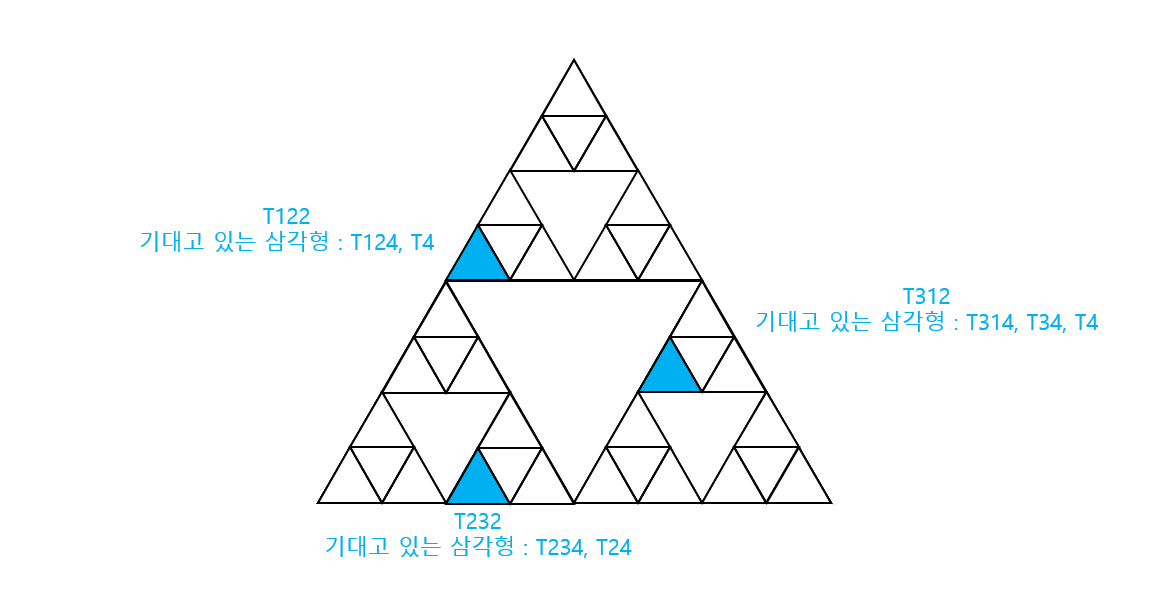
입력된 삼각형의 마지막 부분이 4가 아닐 때는, 기대고 있는 삼각형이 여러 경우로 나올 수 있다.
T312 삼각형처럼, 분할된 삼각형들의 4 삼각형을 전부 기댈 수도 있지만, T122 삼각형이나 T232 삼각형처럼 분할된 삼각형들의 4 삼각형 중 일부는 기대지 않을 수도 있다.

주요 아이디어는, 이전에 동일한 방향으로 분할한 적이 있으면 해당 4 삼각형을 기대지 않는다.
동일한 방향으로 한번 더 분할하면, 해당 4 삼각형과 거리가 멀어지는 아이디어를 사용한다.
T111, T112, T113 삼각형을 예시로 들어보자.
T11[1], T11[2], T11[3] 삼각형은 이전에 동일한 방향으로 분할된 적이 있으니 각자 T114 삼각형을 기댄다.
T1[11] 삼각형은 앞에서 1 방향으로 분할된 적이 있으니, T14 삼각형을 기대지 않는다.
T1[12], T1[13] 삼각형은 앞에서 2나 3 방향으로 분할된 적이 없으니, T14 삼각형을 기댄다.
T[111], T[112], T[113] 삼각형은 앞에서 1 방향으로 분할된 적이 있으니, T4 삼각형을 기대지 않는다.
이 아이디어를 이용해 구현한다.
import sys
input = sys.stdin.readline
a = input().rstrip()
if a[-1] == '4':
print(a[:-1] + '1')
print(a[:-1] + '2')
print(a[:-1] + '3')
else:
for i in range(len(a)-1, 0, -1):
flag = True
for j in range(i + 1, len(a)):
if a[i] == a[j]:
flag = False
break
if flag: print(a[:i] + '4')'-- 예전 기록 > BOJ' 카테고리의 다른 글
| [ BOJ ] 1261 : 알고스팟 ( GOLD 4 ) / Python (0) | 2024.01.04 |
|---|---|
| [ BOJ ] 1005 : ACM Craft ( GOLD 3 ) / Python (0) | 2024.01.02 |
| [ BOJ ] 12796 : 나의 행렬곱셈 답사기 ( GOLD 5 ) / Python (2) | 2024.01.01 |
| [ BOJ ] 1655 : 가운데를 말해요 ( GOLD 2 ) / Python (2) | 2023.12.08 |
| [ BOJ ] 17144 : 미세먼지 안녕! ( GOLD 4 ) / Python (0) | 2023.12.07 |